Определить жесткость k пружины пистолета, если она была сжата на x = 10 см

Пример 1. При выстреле из пружинного пистолета вертикально вверх пуля массой m = 20 г поднялась на высоту h = 5 м. Определить жесткость k пружины пистолета, если она была сжата на x = 10 см. Массой пружины пренебречь.

РЕШЕНИЕ. Воспользуемся законом сохранения энергии в механике. Но прежде проследим за энергетическими превращениями, с которыми связан выстрел. При зарядке пистолета сжимается пружина и совершается работа A₁, в результате чего пружина приобретает потенциальную энергию П₁. При выстреле потенциальная энергия пружины переходит в кинетическую энергию Т₂ пули, а затем при подъеме ее на высоту h превращается в потенциальную энергию П₂ пули.

Если пренебречь потерями энергии в этой «цепочке» энергетических превращений, то на основе закона сохранения энергии можно записать:

A₁ = П₂. (1)

Найдем работу А₁. Сила F₁, сжимающая пружину, является переменной: в каждый момент она по направлению противоположна силе упругости F и численно равна ей. Сила упругости, возникающая в пружине при ее деформации, определяется по закону Гука: F = kx, где x – абсолютная деформация пружины.

Работу переменной силы вычислим как сумму элементарных работ. Элементарная работа при сжатии пружины на dx выразится формулой dA₁ = F₁dx, или dA₁ = kx× dx. Интегрируя в пределах от 0 до x, получим:

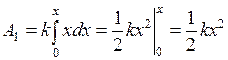. (2)

Потенциальная энергия пули на высоте h определится по формуле:

П₂ = mgh, (3)

где g – ускорение свободного падения.

Подставив в (1) выражение A₁ из (2) и П ₂ из (3), найдем

,

откуда

. (4)

Проверим, дает ли полученная формула единицу жесткости k. Для этого в правую часть формулы (4) вместо величин подставим их единицы:

.

Убедившись, что полученная единица Н/м является единицей жесткости, подставим в формулу (4) значения величин и произведем вычисления:

Пример 2.Через блок в виде сплошного диска, имеющего массу m = 80 г (рис.1), перекинута тонкая гибкая нить, к концам которой подвешены грузы с массами m₁ = 100 г и m ₂ = 200 г. С каким ускорением будут двигаться грузы, если их предоставить самим себе? Трением и массой нити пренебречь.

РЕШЕНИЕ. Воспользуемся основными уравнениями динамики поступательного и вращательного движений. Для этого рассмотрим силы, действующие на каждый груз в отдельности и на блок. На первый груз действуют две силы: сила тяжести и сила упругости (сила натяжения нити) 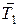. Спроецируем эти силы на ось x, которую направим вниз, и напишем уравнение движения (второй закон Ньютона) в координатной форме:

m₁g – T₁ = – m₁a. (1)

Уравнение движения для второго груза запишется аналогично:

m₂g – T₂ = m₂a. (2)

Рис. 1.

Под действием двух моментов сил Tr и Tr относительно оси, перпендикулярной плоскости чертежа, блок приобретает угловое ускорение e (e = a/r). Согласно основному уравнению динамики вращательного движения

Tr – Tr = J_ze, (3)

где – момент инерции блока (сплошного диска) относительно оси z.

Сила T согласно третьему закону Ньютона по абсолютному значению равна силе T₁. Соответственно сила T по абсолютному значению равна силе T₂. Воспользовавшись этим, подставим в уравнение (3) вместо Tи T выражения для T₁ и T₂, получив их предварительно из уравнений (1) и (2):

.

После сокращения на r и перегруппировки членов найдем интересующее нас ускорение:

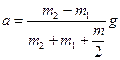. (4)

Отношение масс в правой части формулы (4) есть величина безразмерная. Поэтому массы m₁, m₂ и m можно выразить в граммах, как они даны в условии задачи. Ускорение g надо выразить в единицах СИ. После подстановки получим:

.

Пример 3. Платформа в виде сплошного диска радиусом R = 1,5 м и массой m₁= 180 кг вращается по инерции около вертикальной оси с частотой n = 10 мин^-1. В центре платформы стоит человек массой m₂ = 60 кг. Какую линейную скорость относительно пола помещения будет иметь человек, если он перейдет на край платформы?

РЕШЕНИЕ. Платформа вращается по инерции. Следовательно, момент внешних сил относительно оси вращения z, совпадающей с геометрической осью платформы, равен нулю. При этом условии момент импульса L_z системы платформа – человек остается постоянным:

L_z = J_z w = , (1)

где J_z – момент инерции платформы с человеком относительно оси z; w – угловая скорость платформы.

Момент инерции системы равен сумме моментов инерции тел, входящих в состав системы, поэтому J_z = J₁ + J₂, где J₁ – момент инерции платформы; J₂ – момент инерции человека.

С учетом этого равенство (1) примет вид:

(J₁ + J₂)w = ,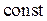

или

(J₁ + J₂)w = (J+J)w¢, (2)

где значения моментов инерции J₁ и J₂ относятся к начальному состоянию системы; J и J к конечному.

Момент инерции платформы относительно оси z при переходе человека не изменяется: J₁ = J = m₁R². Момент инерции человека относительно той же оси будет изменяться. Если рассматривать человека как материальную точку, то его момент инерции J₂ в начальном положении (в центре платформы) можно считать равным нулю. В конечном положении (на краю платформы) момент инерции человека J = m₂R². Подставим в формулу (2) найденные выражения моментов инерции, а также выразим начальную угловую скорость w вращения платформы с человеком через частоту вращения n (w = 2pn) и конечную угловую скорость w¢ – через линейную скорость 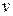человека относительно пола (w¢= /R):

.

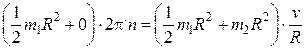После сокращения на R² и простых преобразований находим интересующую нас скорость:

.

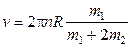Учитывая, что n = 10 мин ^-1 = 1/6 с ^-1, подставим числовые значения физических величин в СИ и произведем вычисления:

.

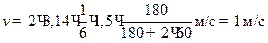Пример 4. В сосуде объемом 20 л находится 4 г водорода при температуре 27°С. Найти давление водорода.

РЕШЕНИЕ. Идеальные газы подчиняются уравнению Менделеева-Клапейрона

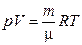, (2)

которое связывает объем газа V, его давление р, термодинамическую температуру Т и массу m. В уравнении (1) R = 8,31 Дж/(моль×К) – газовая постоянная, m – молярная масса газа, n= m/m – количество газа.

Из уравнения (1) имеем

.

Подставляя числовые данные m = 4×10^{-3 кг,} m = 0,002 кг/моль,
Т = 300 К, V = 20 л = 2×10^{-2 м3}, получим:

Пример 5. Найти удельную теплоемкость при постоянном объеме некоторого многоатомного газа, если известно, что плотность этого газа при нормальных условиях равна 0,795 кг/м³.

РЕШЕНИЕ. Удельная теплоемкость при постоянном объеме определяется формулой:

(1)

где R – универсальная газовая постоянная, i – число степеней свободы молекул многоатомного газа и m – молярная масса газа.

Формулу для плотности газа нетрудно получить из уравнения Менделеева-Клапейрона:

(2)

Из (1) и (2) имеем:

(3)

Так как газ находится при нормальных условиях, то
р = 1,013×10⁵ Па, Т = 273 К. Для многоатомных газов i = 6. Подставляя числовые данные в (3), получим:

с_V = 1,4 кДж/(кг×К).

Пример 6. При изотермическом расширении азота массой 100 г, имевшего температуру 280 К, его объем увеличился в 3 раза. Найти: работу, совершенную газом при расширении; изменение внутренней энергии газа; количество теплоты, сообщенное газу.

Решение. Из уравнения Менделеева-Клапейрона находим:

При изотермическом процессе (T = const), работа газа определяется по формуле

.

Молярная масса азота m = 28∙10^-3 кг/моль, V₂/V₁ = 3, m = 0,1 кг,
R = 8,31 Дж/(моль∙К). Подставив в последнюю формулу числовые значения, получим A = 9,13 кДж.

Изменение внутренней энергии ∆U = 0, так как T = const. Следовательно, согласно первому закону термодинамики, сообщенное газу количество теплоты Q = A = 9,13 кДж.