Показатели изменчивости

Изучение и количественное описание изменчивости (вариации) осуществляется различными методами, и можно сказать, что разработанные в математической статистике методы анализа экспериментальных данных в значительной своей части предназначены именно для оценки вариации.

Размах вариации. Это показатель, представляющий собой разность максимальной и минимальной вариант совокупности. Чем сильнее варьирует признак, тем больше размах вариации и наоборот.

Р = Х_max – X_min

Лимиты и размах вариации - простые и наглядные характеристики варьирования, однако им присущи существенные недостатки: при повторных измерениях одного и того же группового объекта они могут существенно изменяться; кроме того, они не отображают существенные черты варьирования.

Более удобной характеристикой вариации мог бы служить показатель, который строится на основании отклонений вариант от их средней. Сумма таких отклонений, взятая без учета знаков и отнесенная к числу наблюдений, называется средним линейным отклонением.

Дисперсия и ее свойства. Несмотря на явное преимущество среднего линейного отклонения перед лимитами и размахом вариации, этот показатель не получил широкого распространения на практике. Наиболее подходящим оказался показатель, построенный не на отклонениях вариант от их средних, а на квадратах этих отклонений, его называют дисперсией (рассеяние) и выражают формулой .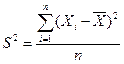

Ценность дисперсии заключается в том, что, являясь мерой варьирования числовых значений признака вокруг их средней арифметической, она измеряет и внутреннюю изменчивость значений признака, зависящую от разностей между наблюдениями. Преимущество дисперсии перед другими показателями вариации состоит также в том, что она разлагается на составные компоненты, позволяя тем самым оценивать влияние различных факторов на величину учитываемого признака.

Вместе с тем установлено, что рассчитываемая по формуле дисперсия оказывается смещенной по отношению к своему генеральному параметру на величину, равную n/n-1. Чтобы получить несмещенную дисперсию, нужно в формулу ввести в качестве множителя поправку на смещенность, называемую поправкой Бесселя. В результате 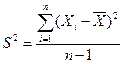Разность n-1 называют числом степеней свободы, под которым понимают число свободно варьирующих единиц в составе численно ограниченной статистической совокупности.

Дисперсия обладает рядом важных свойств, из которых необходимо выделить следующие.

1. Если каждую варианту совокупности уменьшить или увеличить на одно и то же постоянное число, то дисперсия не изменится.

2. Если каждую варианту совокупности умножить или разделить на одно и то же постоянное число А, то дисперсия уменьшится или увеличится в А² раз.

Среднее квадратичное отклонение (S) Наряду с дисперсией важнейшей характеристикой варьирования является среднее квадратичное отклонение - показатель, представляющий корень квадратный из дисперсии.

Эта величина в ряде случаев оказывается более удобной характеристикой варьирования чем дисперсия, так как выражается в тех же единицах, что и средняя арифметическая.

Коэффициент вариации. Рассмотренные до сих пор показатели изменчивости: размах, дисперсия, стандартное отклонение определяют вариацию в абсолютных единицах, имеют размерность такую же или в квадрате (для дисперсии), как и сама измеряемая величина. При описании распределений численности это удобно, но если есть необходимость сравнить показатели рассеяния двух распределений, данные которых имеют разные размерности, то естественно возникают затруднения. Такие же затруднения возникают иногда даже в тех случаях, когда измеряемые величины имеют одну и ту же размерность. Например, показатели рассеяния в распределениях количества выпавших осадков и роста людей вычислены в сантиметрах. Однако из того, что стандартное отклонение роста людей больше, чем стандартное отклонение выпавших осадков, не следует, что изменчивость в первом случае больше. Меры изменчивости при сравнении показательны лишь в соотношении со средними, от которых измеряют отклонения. Поэтому возникает необходимость в таком показателе рассеяния, который был бы безразмерным и указывал на изменчивость по отношению к среднему, относительно которого вычисляются отклонения. Наиболее часто используемым показателем, удовлетворяющим этим требованиям, является коэффициент вариации .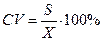

Из формулы видно, что на величину коэффициента вариации влияет как стандартное отклонение, так и среднее. Причем так как среднее стоит в знаменателе, при стремлении его к нулю коэффициент вариации становится неопределенным. Поэтому для распределений численностей со средними, близкими к нулю, использование коэффициента вариации в качестве показателя изменчивости нежелательно.