Количественная оценка результатов эксперимента.
Явления, интересующие исследователя, должны изучаться в их взаимосвязи, в зависимости от их структуры, соотношений, в которых они находятся между собой и пр. Для целостного изучения явлений, статистика выработала показатели, известные под названием показателей относительной доли или показателей структуры и показателей соотношения. Эти показатели даются в процентах, промилле, продецимилле и т. д.
Так как наблюдаемый признак в каждом отдельном случае может быть, а может не быть, то такие признаки называются альтернативными, а их обозначение при помощи статистических показателей и анализ этих показателей называется альтернативным анализом.
Техника вычисления относительных величин не трудна (она связана только с действием деления). При анализе же этих показателей часто допускаются ошибки. На некоторых из них следует остановиться.
Для того, чтобы проанализировать типы допускаемых ошибок, следует дать классификацию соответствующих показателей. В общей форме можно назвать 2 категории: показатели структуры и показатели соотношения.
Показатели структуры называются иначе экстенсивными показателями. Их можно разделить на 2 группы: экстенсивно-расчленительные и экстенсивно-указательные. Первые отражают выраженное в процентах соотношение между частью и целым, а вторые - выраженное также в процентах отношение между частями целого.
Из 500 случайно отобранных листьев 450 без повреждений, а остальные погрызены вредителями. В этом случае экстенсивно-расчленительный показатель равен (450/500)×100=90 %. Этот процент, дающий представление о структуре совокупности, составляют целые. Экстенсивно-указательный показатель будет обозначать отношение целых к погрызенным: (450/50)×100=900 %. Это число показывает, что на 100 погрызенных приходится 900 целых. Иногда экстенсивно-указательные величины вычисляются не в процентах. В приведенном выше примере (450/50)=9 эта цифра показывает, что на 1 испорченный вредителями лист приходится 9 целых. При экстенсивно-указательных величинах не имеет значения какая цифра будет в числителе, а какая в знаменателе. Во взятом примере можно дать отношение и в форме (50/450)=0,11. Изменится только толкование (на один целый приходится 0,11 испорченных).
Показатели соотношения называются также частотами, потому что они показывают частоту изучаемых явлений. Эти показатели можно разделить на 2 категории: интенсивные и координационные показатели. Интенсивные представляют собой соотношение между числом случаев некоторого события и средой, в которой это событие наступает. Координационные же представляют соотношение между числом случаев в двух явлениях, между которыми существует непрямая связь.
В городе Кемерове 100000 детей школьного возраста, население - 500000 человек, а число преподавателей 2000 человек. Требуется вычислить показатель, отражающий количество учеников в составе взрослого населения, и показатель обеспеченности населения учителями.
Так как событием является вступление ребенка в школьный возраст, а средой, в которой оно происходит, - население, то первый показатель будет равняться (100000/500000) ×1000=200 на 1000 населения.
Координационным показателем обеспеченности населения учителями является отношение между численностью населения и числом преподавателей. Он может быть вычислен двумя способами: (500000/2000)=225 или (2000/500000) ×1000=4. Толкование этих показателей таково: 1) один учитель приходится на 225 человек или 2) на 1000 человек населения приходится 4 преподавателя.
Предложенная классификация дает возможность лучше понять природу ошибок, допускаемых при вычислении относительных показателей.
Не следует забывать, что за вычисленными относительными величинами стоят конкретные данные. Иногда 1 % какого-либо показателя по своему значению равняется 10 % того же показателя, вычисленного для другого объекта. Поэтому при составлении статистических таблиц необходимо вместе с процентными числами приводить и абсолютные числа.
Показатели относительной доли не рекомендуется суммировать или усреднять (кроме некоторых специальных случаев).
Экстенсивно-указательные величины показывают процентное отношение между частями одного и того же целого, поэтому здесь возможен результат как меньший, так и больший 100 %. При вычислении этих показателей необходимо обращать внимание на следующее: окончательный результат различен в зависимости от того, какая из частей целого помещена в числитель, а какая в знаменатель. Рекомендуется в этом случае обращать внимание не на разность в процентах, а на их соотношения, а эти соотношения равны. В первом примере, 11,1(1) % и 900 %. В данном случае (900/100)=9 и (100/11,1(1))=9, т.е. в первом случае в 9 раз меньше, а во втором в 9 раз больше 100 %.
При вычислении интенсивных статистических показателей необходимо тщательно определять среду, в которой происходят изучаемые события. Это определение в некоторых случаях затрудняется тем, что не всегда можно количественно учесть среду. Например, при изучении показателя смертности необходимо знать не только число умерших, но и число заболевших. Однако, в то время как об умерших можно иметь точные данные (на каждого умершего составляется акт о смерти, в который вписана причина смерти), точное число заболевших часто не известно.
Иногда, чтобы избежать этой трудности, вычисление интенсивных статистических показателей заменяется вычислением экстенсивных, что приводит к ошибочным выводам.
Порядок изменения экстенсивных показателей не всегда соответствует порядку изменения интенсивных.
Следует быть особенно осторожными при вычислении показателей относительной доли при малочисленных выборках. Например, решено проверить воздействие определенного токсического вещества только в одном эксперименте. В этом случае возможны только 2 варианта: испытуемое животное или умрет, или не умрет, т.е. для оценки эффекта процент может быть или 0, или 100. В первом случае недооценивается действие испытуемого вещества, во втором оно переоценивается.
При пользовании процентами, являющимися мерой-эталоном сравнения, надо знать основание, в отношении которого они вычислены. Это особенно важно когда имеют дело с так называемой многократной манипуляцией и процентами.
Изучая некоторые явления при помощи интенсивных статистических показателей, сталкиваются с фактом, что величина этих показателей не зависит от структуры среды, в которой имеют место изучаемые явления. Так, например, смертность выше в тех населенных пунктах, в которых число детей раннего детского возраста и стариков больше, потому что среди них смертность наиболее высока.
При таких и подобных им случаях при сравнении интенсивных статистических показателей, вычисленных для среды с различной структурой, необходимо применять так называемый метод стандартизации.
Метод стандартизации ставит себе задачей унифицировать структуру среды, в отношении которой вычисляются интенсивные статистические показатели. Различаются прямой и косвенный методы стандартизации. Прямой метод применяется в тех случаях, когда известны абсолютные числа, характеризующие изучаемое явление, а также среду, в которой оно происходит.
Эти числа необходимо знать раздельно для частей той среды, которая оказывает влияние на величину интенсивных показателей.
Эти числа необходимо знать раздельно для частей той среды, которая оказывает влияние на величину интенсивных показателей. Косвенный метод применяется в тех случаях, когда известна только общая численность изучаемого явления.
Пример. В 1931г. смертность среди служителей культа и шахтеров в Уэльсе была такова
| Возрастные группы | Духовенство | Шахтеры | Стандарт L | Стандартизованные коэффициенты | |||||
| Всего | умерли | смертность | всего | умерли | смертность | духовенство | шахтеры | ||
| 16-24 | 200 | 0 | 0 | 70000 | 259 | 3.7 | 22.0 | 0 | 81.4 |
| 25-34 | 2300 | 0 | 0 | 131000 | 524 | 4.0 | 22.0 | 0 | 88.00 |
| 35-44 | 3600 | 16 | 4.4 | 102000 | 663 | 6.5 | 17.9 | 78.76 | 116.35 |
| 45-54 | 4900 | 28 | 5.6 | 77000 | 939 | 12.2 | 16.4 | 91.84 | 200.08 |
| 55-64 | 5300 | 95 | 17.8 | 49000 | 1279 | 26.2 | 12.6 | 224.28 | 330.12 |
| старше 65 | 6400 | 490 | 76.6 | 31000 | 3026 | 97.6 | 9.1 | 697.06 | 888.16 |
| Всего | 22700 | 629 | 27.7 | 460000 | 6690 | 14.5 | 100.0 | 1091.94 | 1704.11 |
Если по этим числам вычислить интенсивные статистические показатели смертности, то окажется, что у служителей культа она выше P1=27.7 на 1000 человек (629/22700)*1000; а у шахтеров она ниже P2=14.5=(6690/ /460000)*1000. Однако эти показатели выведены для профессий имеющих различный возрастной состав. Если вычислить показатели смертности для отдельных возрастных групп, то окажется, что смертность шахтеров гораздо выше. Следовательно необходимо применить метод стандартизации для того, чтобы унифицировать возрастную структуру этих двух групп населения. Для использования прямого метода стандартизации необходимо избрать некоторый условный стандарт. В качестве такого стандарта в данном случае избран возрастной состав мужского населения Уэльса в возрасте 16 лет и старше. После этого рассчитываются стандартизованные коэффициенты для отдельных возрастных групп по формуле (P*L).
Эти коэффициенты исчисляются отдельно для обоих групп населения: полученные таким образом цифры суммируются и делятся на 100. Получаются стандартизованные коэффициенты смертности, в которых устранено влияние различной возрастной структуры. В данном примере стандартизованный коэффициент смертности служителей культа составляет 10.92 на 1000, а шахтеров 17.04 на 1000. Следовательно, первоначальное заключение должно быть изменено.
В научных исследованиях применяют два вида статистического исследования: сплошное и выборочное. При выборочном исследовании наблюдение ведется только за частью случаев, входящих в объект исследования, а полученные результаты обобщаются применительно ко всем случаям. Выборочные исследования имеют ряд преимуществ: они дешевле, проводятся в более короткие сроки, а в некоторых случаях являются единственной возможной формой исследования. Однако, так как эти наблюдения не являются сплошными, в них всегда имеется некоторая неточность, называемая ошибкой репрезентативности.
При наблюдении над 100 непреднамеренно подобранными студентами было установлено, что 90 из них любят конфеты (т.е. 90 %) . Так как эта величина получена при относительно малом количестве человек, то возникает вопрос: если провести другие такие же наблюдения, будет ли получен тот же процент.
Очевидно - нет. Следовательно, если поставить вопрос о количестве любителей сладкого, то дать на него ответ в виде точно определенного процента нельзя, можно лишь указать интервал, в границах которого находится интересующий исследователя процент. Этот интервал определяется следующим образом. Его нижняя граница равна Р-D, а верхняя Р+D, где Р - полученный процент, D- размер неточности, допущенной вследствие несплошного характера наблюдения. Эту величину находят по следующей формуле:
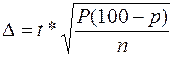 , где n - число наблюдаемых случаев, Р - найденный процент; t - в этом случае представляет собой так называемый доверительный коэффициент. При вероятности Р=0,95 (t=1,96), при Р=0,99 (t=2,58).
, где n - число наблюдаемых случаев, Р - найденный процент; t - в этом случае представляет собой так называемый доверительный коэффициент. При вероятности Р=0,95 (t=1,96), при Р=0,99 (t=2,58).
В использованном примере при доверительной вероятности Р=0,95 и t=1,96. 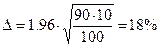
Видоизменяя формулу, например, можно рассчитать необходимое число наблюдений для получения определенного размера неточности: 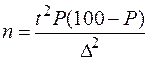 .
.
В условиях предыдущей задачи найти число наблюдений, чтобы ошибка не превышала 4 %
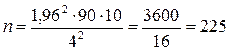
Вопросы для самопроверки:
1. Приведите примеры, которые, как вам кажется, иллюстрируют неправильные применения расчета средних величин.
2. Может ли оказаться что: а) значение дисперсии равно значению стандартного отклонения? б) значение дисперсии меньше значения стандартного отклонения?
3. Как изменения ряда экспериментальных данных воздействуют на среднее?
4. Как соотносятся среднее, мода и медиана для распределений смещенных влево (вправо)?
5. Приведите примеры неправильного использования процентов.
6. Рыбак за час поймал 20 рыб, из которых 8 караси. Определите с 95% вероятностью диапазон времени, которое он затратит на поимку 20 карасей.
Дата добавления: 2020-10-01; просмотров: 552;











