Показатели центральной тенденции. Средние.

В отличие от индивидуальных числовых характеристик средние величины обладают большей устойчивостью, способностью характеризовать целую группу одним (средним) числом.

В зависимости от того, как распределены исходные данные - в равно- или неравноинтервальный вариационный ряд, для их характеристики применяют разные средние величины. Именно при распределении собранных данных в неравноинтервальный вариационный ряд более подходящей обобщающей характеристикой изучаемого объекта служит так называемая плотность распределения, т. е. отношение частот или частостей к ширине классовых интервалов. Кроме того, числовыми характеристиками таких рядов могут служить средние из абсолютных или относительных показателей плотности распределения. Средняя плотность показывает, сколько единиц данной совокупности приходится в среднем на интервал, равный единице измерения учитываемого признака.

В качестве статистических характеристик равноинтервальных вариационных рядов применяют средние величины.

Средняя арифметическая. Этот показатель является центром распределения, вокруг которого группируются все варианты статистической совокупности. Средняя арифметическая может быть простой и взвешенной. Простую арифметическую определяют как сумму всех членов совокупности, деленную на их общее число.

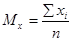
Когда отдельные варианты повторяются, среднюю арифметическую вычисляют по формуле: 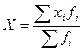и называют взвешенной средней.

Имеется распределение учета численности косуль за апрель 2003г. Требуется вычислить среднее количество косуль за учет.

X=(7+20+12+12+15)/30=66/30=2.02.