Показатели асимметрии и эксцесса

При анализе распределения численностей значительный интерес представляет оценка отклонения данного распределения от симметричного, или, иначе говоря, его скошенность. Степень скошенности (асимметрия) является одним из наиболее важных свойств распределения численностей. Существует целый ряд статистических показателей, предназначенных для вычисления асимметрии. Все они отвечают, как минимум, двум требованиям, предъявляемым к любому показателю скошенности: он должен быть безразмерным и равным нулю, если распределение симметрично.

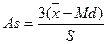
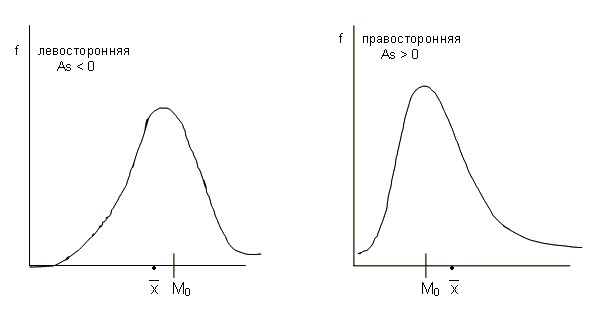
Из этой формулы следует, что распределения, скошенные влево, имеют положительную асимметрию, а скошенные вправо — отрицательную. Естественно, что для симметричных распределений, для которых среднее и медиана совпадают, асимметрия равна нулю.

Известно, что величина As, определяемая по формуле, находится в интервале [-3,3]. Но практически эта величина очень редко достигает своих крайних значений, и для умеренно асимметричных одновершинных распределений она по модулю обычно меньше единицы.

Показатель асимметрии может быть использован не только для формального описания распределения численностей, но и для содержательной интерпретации полученных данных.

В самом деле, если наблюдаемый нами признак формируется под воздействием большого числа независимых друг от друга причин, каждая из которых вносит относительно небольшой вклад в величину этого признака, то в соответствии с некоторыми теоретическими предпосылками, обсуждавшимися в разделе по теории вероятностей, вправе ожидать, что получаемое в результате эксперимента распределение численностей будет симметричным. Однако если для экспериментальных данных получена значительная величина асимметрии (большая по абсолютной величине, чем 0,5), то можно предположить, что условия, указанные выше, не соблюдаются.

В этом случае имеет смысл предположить либо существование какого-то одного или двух факторов, вклад которых в формирование наблюдаемой в эксперименте величины существенно больше, чем остальных, либо постулировать наличие специального механизма, отличного от механизма независимого влияния множества причин на величину наблюдаемого признака.

Так, например, если изменения интересующей нас величины, соответствующие действию некоторого фактора, пропорциональны самой этой величине и интенсивности действия причины, то получаемое при этом распределение будет всегда скошено влево, иметь положительную асимметрию. С таким механизмом сталкиваются, например, биологи, оценивая величины, связанные с ростом растений и животных.

Другой способ оценки асимметрии основан на методе моментов.

.

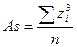Таким образом, мера скошенности представляет собой среднее значение стандартизованных данных, возведенных в куб.

Показатели асимметрии, вычисленные по разным формулам, отличаются друг от друга по величине, но одинаково указывают на характер скошенности. В пакетах прикладных программ для статистического анализа при расчете асимметрии используют последнюю формулу.

Эксцесс

Итак, мы рассмотрели три из четырех групп показателей, с помощью которых описываются распределения численностей. Последней из них является группа показателей островершинности, или эксцесса. Для вычисления одного из возможных показателей эксцесса используется следующая формула:

.

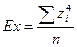Величина эксцесса для нормальной (гауссовой) кривой распределения, играющей в статистике, так же как и в теории вероятностей большую роль, равна 3. Исходя из целого ряда соображений заостренность этой кривой принимают за стандарт, и поэтому в качестве показателя эксцесса используют величину γ=Ех - 3.

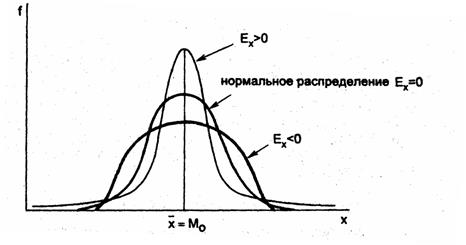
Эксцесс может принимать очень большие значения, , но он не может быть меньше единицы. Оказывается, что если распределение двувершинно (бимодально), то значение эксцесса близко к единице, так что γ близко к -2. Экспериментально установлено, что если значение γ меньше -1,4 , то можно быть уверенным, что имеющееся в нашем распоряжении распределение по крайней мере бимодально. Это особенно важно учитывать, когда эспериментальные данные, минуя стадию предварительной обработки, анализируются с помощью ЭВМ и перед глазами исследователя нет графического изображения распределения численностей.