Проверка гипотезы о законе распределения
Большое познавательное значение имеет сопоставление фактических кривых распределения с теоретическими.
Под теоретической кривой распределения понимается графическое изображение ряда в виде непрерывной линии изменения частот в вариационном ряду, функционально связанного с изменением вариантов (значений признака). Теоретическое распределение может быть выражено аналитически - формулой, которая связывает частоты вариационного ряда и соответствующие значения признака. Такие алгебраические формулы носят название законов распределения
Гипотезы о распределениях заключаются в том, что выдвигается предположение о том, что распределение в генеральной совокупности подчиняется какому-то определенному закону. Проверка гипотезы состоит в том, чтобы на основании сравнения фактических (эмпирических) частот с предполагаемыми (теоретическими) частотами сделать вывод о соответствии фактического распределения гипотетическому распределению. Может проводиться и сравнение частостей.
Под гипотетическим распределением необязательно понимается нормальное распределение. Может быть выдвинута гипотеза о биномиальном распределении, распределении Пуассона и т.д. Причина частого обращения к нормальному распределению в том, что в этом типе распределения выражается закономерность, возникающая при взаимодействии множества случайных причин, когда ни одна из них не имеет преобладающего влияния. Закон нормального распределения лежит в основе многих теорем математической статистики, применяемых для оценки репрезентативности выборок, при измерении связей и т. д.
Итак, пусть имеется вариационный ряд. Предположим, что признак Х распределен по некоторому вероятностному закону Р. 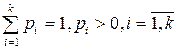
| х | х1 | х2 | .... | xk |
| р | p1 | p2 | ..... | pk |
По теоретическому распределению Р можно построить так называемое выравнивающие или теоретические частоты 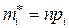 . Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.
. Если отличия между теоретическими и эмпирическими частотами небольшое, то можно считать, что Х распределен по закону Р.
χ2 Пирсона
Критерий согласияχ2 разработан достаточно хорошо и поэтому используется достаточно часто. Он основан на сравнении эмпирических частот интервалов группировки с теоретическими (ожидаемыми) частотами, рассчитываемыми по формулам нормального распределения.
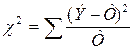
Если все эмпирические частоты равны соответствующим теоретическим частотам, то χ2 равно нулю. Очевидно, что чем больше отличаются эмпирические и теоретические частоты, тем χ2 больше; если расхождение несущественно, то χ2 должно быть малым.
Гипотезы-
Н0: Различия между двумя распределениями недостоверны.
H1: Различия между двумя распределениями достоверны.
Существуют табличные значения (см. приложение) для соответствующего числа степеней свободы К и уровня значимости 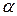 . По таблице находятся
. По таблице находятся 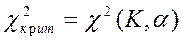 K=k-1-r, где r - число общих характеристик теоретического распределения, принятых равными соответствующим эмпирическим.
K=k-1-r, где r - число общих характеристик теоретического распределения, принятых равными соответствующим эмпирическим.
λ - критерий Колмогорова-Смирнова
Назначение критерия
Критерий λпредназначен для сопоставления двух распределений:
а) эмпирического с теоретическим, например, равномерным или нормальным;
б) одного эмпирического распределения с другим эмпирическим распределением.
Критерий позволяет найти точку, в которой сумма накопленных расхождений между двумя распределениями является наибольшей, и оценить достоверность этого расхождения.
Если в методе χ2 мы сопоставляли частоты двух распределений отдельно по каждому разряду, то здесь мы сопоставляем сначала частоты по первому разряду, потом по сумме первого и второго разрядов, потом по сумме первого, второго и третьего разрядов и т. д. Таким образом, мы сопоставляем всякий раз накопленные к данному разряду частоты.
Гипотезы-
Н0: Различия между двумя распределениями недостоверны (судя по точке максимального накопленного расхождения между ними).
H1: Различия между двумя распределениями достоверны (судя по точке максимального накопленного расхождения между ними).
Если различия между двумя распределениями существенны, то в какой-то момент разность накопленных частот достигнет критического значения, и мы сможем признать различия статистически достоверными. В формулу критерия λвключается эта разность. Чем больше эмпирическое значение λ, тем более существенны различия.
Дата добавления: 2020-10-01; просмотров: 561;











