Распределение Пуассона

Пусть в нашем распоряжении имеется биномиальная случайная величина с параметрами n и р, распределение вероятностей которой задается формулой биноминального распределения. Предположим, что n неограниченно увеличивается, а параметр р стремится к нулю таким образом, что произведение n*p=λ остается постоянным. Тогда,

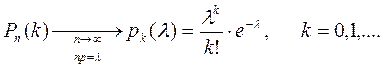
Теперь вернемся к численной оценке вероятности обнаружения в случайной популяции из 5000 людей ровно пяти человек, страдающих неким заболеванием, встречающимся с частотой 0,001. Используя пуассоновское приближение биномиального распределения, имеем (λ=n*p=5):

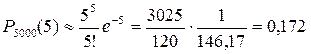
Числовые характеристики дискретных случайных величин

Математическое значение дискретной случайной величины Х, имеющее конечное число возможных значений, равно

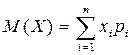
Дисперсия дискретной случайной величины Х, имеющее конечное число возможных значений, равно

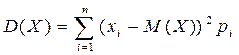или

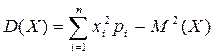
Дискретная случайная величина задана рядом распределения:

M(X)=1*0.1+2*0.3+4*0.6=3.1

D(X)=(1-3.1)²*0.1+(2-3.1)²*0.3+(4-3.1)²*0.6=1.29

Или по второй формуле

D(X)=1²*0.1+2²*0.3+4²*0.6-3.1²=1.29