Закон распределения случайной величины
Закон распределения считается заданным, если известны:
· множество возможных значений случайной величины;
· способ количественного определения вероятности попадания случайной величины в произвольную область этого множества.
Пусть на плоскость бросают два тела, имеющие форму тетраэдра, грани которого занумерованы числами 1, 2, 3, 4. Допустим, что для каждого тетраэдра вероятность упасть на любую грань равна 1/4. В этом случае, если бросания тетраэдров выполняются независимо, то вероятность получить, например, результат (2,4), т. е. вероятность того, что первый тетраэдр упадет на грань 2, второй - на грань 4, равна (1/4)(1/4) = 1/16. Аналогично вычисляются и вероятности других исходов, так что каждый из 16 элементарных исходов имеет вероятность 1/16. На этом же пространстве элементарных исходов определим некоторую величину У, которая будет называться случайной величиной и значения которой у представляют собой суммы чисел, стоящих на нижних гранях тетраэдра.
| (1,1)=2 (1,2)=3 (1,3)=4 (1,4)=5 | (2,1)=3 (2,2)=4 (2,3)=5 (2,4)=6 | (3,1)=4 (3,2)=5 (3,3)=6 (3,4)=7 | (4,1)=5 (4,2)=6 (4,3)=7 (4,4)=8 |
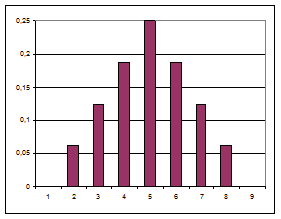
Используя данные этой таблицы, легко получить распределение вероятностей f(y) случайной величины y.
| Y | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| p(y) | 1/16 | 2/16 | 3/16 | 4/16 | 3/16 | 2/16 | 1/16 | |
| 
| |||||||
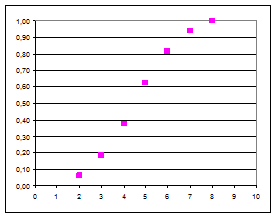
| Элементарные исходы и соответствующие значения y | График функции распределения | |||||||
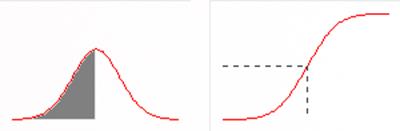
Функция F(x) = р(Х < х), определенная на множестве всех вещественных чисел х и задающая вероятность того, что случайная величина X не превзойдет х, называется функцией распределения
Если X — случайная величина, то каково бы ни было вещественное число х, существует функция f(x) = р(Х = х), задающая вероятность того, что X принимает значение х. Эта функция определяет распределение частот и носит название плотности вероятности.
Функция распределения непрерывной случайной величины связана с плотностью вероятности следующим отношением:
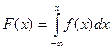
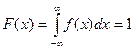
| 
|
Для дискретных случайных величин плотность распределения определяется набором вероятностей для отдельных дискретных значений в пространстве элементарных событий.
Дата добавления: 2020-10-01; просмотров: 661;











