Разложение функций в степенные ряды

Пусть дана функция f(x), которую требуется разложить в степенной ряд, т.е. представить в виде (30):

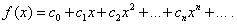
Задача состоит в определении коэффициентов 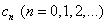ряда (30). Для этого, дифференцируя равенство (30) почленно, последовательно найдём:

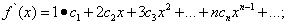
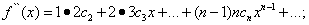
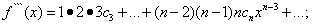
……………………………………………….. (31)

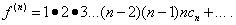
Полагая в равенствах (30) и (31) х = 0, находим

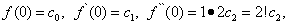
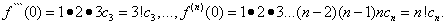
Тогда

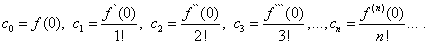
Подставляя найденные выражения в равенство (30), получим

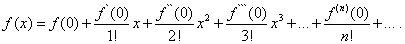(32)

Это разложение функции f(x) в ряд называется рядом Маклорена.

Найдём разложение в ряд Маклорена некоторых элементарных функций.

ВОПРОС 56. Задачи, приводящие к дифференциальным уравнениям (экономика, социология и др.). Дифференциальные уравнения первого порядка. Теорема существования и единственности решения для уравнения первого порядка.

Теорема существования и единственности решения задачи Коши (теорема Коши)

Если уравнение функции f(x) и ее частная производная df/dy непрерывны в некоторой области Д, то данное уравнение имеет единственное решение удовлетворяющее условию y(x₀)=y₀

В точках плоскости, в которых нарушены условия теоремы Коши, называются особыми точками дифференциального уравнения. В этих точках терпит разрыв либо функция f(x,y) либо ее производная. Через каждую из таких точек может проходить либо несколько интегральных кривых, либо не проходит не одной.

Если линия состоит только из особых точек и является интегральной кривой ДУ, то функция y=φ(x) называется особым решением дифференциального уравнения.

Для того, чтобы найти особое решение ДУ, надо найти линию y=φ(x), в каждой точке которой терпит разрыв функция f(x,y) или ее производная, проверить является ли функция y=φ(x) решением данного уравнения.

Особое решение не содержится в общем решении , и не может быть выделено из него ни при каком конкретном значении с.

Разрешив уравнение F(x, y, y’)=0 относительно y’ (если возможно), получим уравнение y’=f(x,y), которое называется дифференциальным уравнением первого порядка.

Общий вид дифференциального уравнения первого порядка:

P(x,y)dx + Q(x,y)dy=0

Геометрический смысл дифференциального уравнения первого порядка:

Угловой коэффициент касательной к интегралу кривой в каждой ее точке равен значению в этой точке правой части дифференциального уравнения y’=f(x,y).

Функция y=φ(x,c), зависящая от аргумента x и произвольной постоянной с называется общим решением ДУ в некоторой области Д, если она удовлетворяет двум условиям:

1. Она удовлетворяет уравнению при любых конкретных значениях с

2. Каково бы ни было задано условие y(x₀)=y₀, можно найти такое значение с = с₀, что функция y=φ(x,c₀) удовлетворяла этому условию.

Если общее решение ДУ задано в неявном виде, то оно называется общим интегралом дифференциального уравнения.

Частным решением ДУ называется любая функция y=φ(x,c₀), которая получается из общего решения y=φ(x,c), при конкретном значении с.

Задача нахождения частного решения ДУ, удовлетворяющего заданному начальному условию, называется задачей Коши.

Решить дифференциальное уравнение значит найти его общее решение или общий интеграл, если не заданы начальные условия, или найти то частное решение, которое удовлетворяет заданному начальному условию.

ВОПРОС 57. Общее решение уравнения первого порядка. Задача Коши для дифференциального уравнения первого порядка, её геометрический смысл. Частное решение уравнения первого порядка.

Геометрический смысл дифференциального уравнения первого порядка:

Угловой коэффициент касательной к интегралу кривой в каждой ее точке равен значению в этой точке правой части дифференциального уравнения y’=f(x,y).

Функция y=φ(x,c), зависящая от аргумента x и произвольной постоянной с называется общим решением ДУ в некоторой области Д, если она удовлетворяет двум условиям:

1. Она удовлетворяет уравнению при любых конкретных значениях с

2. Каково бы ни было задано условие y(x₀)=y₀, можно найти такое значение с = с₀, что функция y=φ(x,c₀) удовлетворяла этому условию.

Если общее решение ДУ задано в неявном виде, то оно называется общим интегралом дифференциального уравнения.

Частным решением ДУ называется любая функция y=φ(x,c₀), которая получается из общего решения y=φ(x,c), при конкретном значении с.

Задача нахождения частного решения ДУ, удовлетворяющего заданному начальному условию, называется задачей Коши.

Решить дифференциальное уравнение значит найти его общее решение или общий интеграл, если не заданы начальные условия, или найти то частное решение, которое удовлетворяет заданному начальному условию.

Теорема существования и единственности решения задачи Коши (теорема Коши)

Если уравнение функции f(x) и ее частная производная df/dy непрерывны в некоторой области Д, то данное уравнение имеет единственное решение удовлетворяющее условию y(x₀)=y₀

В точках плоскости, в которых нарушены условия теоремы Коши, называются особыми точками дифференциального уравнения. В этих точках терпит разрыв либо функция f(x,y) либо ее производная. Через каждую из таких точек может проходить либо несколько интегральных кривых, либо не проходит не одной.

Если линия состоит только из особых точек и является интегральной кривой ДУ, то функция y=φ(x) называется особым решением дифференциального уравнения.

Для того, чтобы найти особое решение ДУ, надо найти линию y=φ(x), в каждой точке которой терпит разрыв функция f(x,y) или ее производная, проверить является ли функция y=φ(x) решением данного уравнения.

Особое решение не содержится в общем решении , и не может быть выделено из него ни при каком конкретном значении с.

Дифференциальное уравнение первого порядка, содержит:
1) независимую переменную ;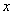
2) зависимую переменную 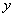(функцию);
3) первую производную функции: .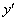

В некоторых случаях в уравнении первого порядка может отсутствовать «икс» или (и) «игрек» – важно чтобы в ДУ была первая производная 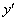, и не было производных высших порядков – 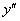, 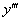и т.д.

Что значит решить дифференциальное уравнение? Решить дифференциальное уравнение – это значит, найти множество функций 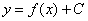, которые удовлетворяют данному уравнению. Такое множество функций называется общим решением дифференциального уравнения.

ВОПРОС 58. Дифференциальные уравнения высших порядков. Общее и частное решения дифференциального уравнения. Теорема существования и единственности решения уравнения второго порядка.

Обыкнове́нныедифференциа́льныеуравне́ния (ОДУ) — это дифференциальное уравнение вида

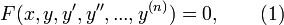
где 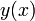— неизвестная функция (возможно, вектор-функция, тогда , как правило, тоже вектор-функция со значениями в пространстве той же размерности; в этом случае говорят о системе дифференциальных уравнений), зависящая от независимой переменной 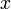, штрих означает дифференцирование по 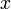. Число 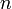(порядок старшей производной, входящей в данное уравнение) называется порядком дифференциального уравнения (1).

Независимая переменная 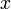часто интерпретируется (особенно в дифференциальных уравнениях, возникающих в физических и других естественно-научных задачах) как время, поэтому её часто обозначают буквой 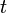. Переменная 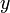— некоторая величина (или совокупность величин, если 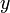является вектор-функцией), изменяющихся со временем. Например, 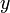может означать набор координат точки в пространстве; в этом случае уравнение (1) описывает движение точки в пространстве, то есть изменение её координат с течением времени. Независимая переменная 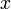обычно принимает вещественные значения, однако рассматриваются и дифференциальные уравнения, в которых переменная 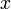комплексная (так называемые уравнения с комплексным временем).

Наиболее часто встречаются дифференциальные уравнения вида

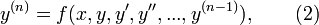
в которых старшая производная 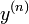выражается в виде функции от переменных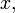 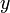и производных 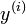порядков меньше 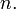Такие дифференциальные уравнения называются нормальными или разрешёнными относительно производной.

В противоположность уравнениям вида (2), дифференциальные уравнения вида (1) называются уравнениями, не разрешёнными относительно производной или неявными дифференциальными уравнениями.

Классическим решением дифференциального уравнения (2) называется 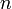раз дифференцируемая функция 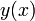, удовлетворяющая уравнению во всех точках своей области определения. Обычно существует целое множество таких функций, и для выбора одного из них требуется наложить на него дополнительное условие. Начальным условием для уравнения (2) называется условие

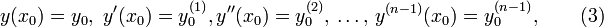
где 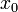— некоторое фиксированное значение независимой переменной (фиксированный момент времени), а 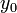и 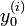— соответственно, фиксированные значения функции 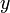и всех её производных до порядка 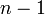включительно. Дифференциальное уравнение (2) вместе с начальным условием (3) называется начальной задачей или задачей Коши:

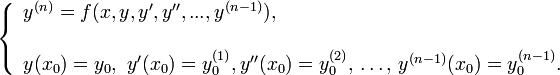
При достаточно общих ограничениях на функцию 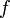, стоящую в правой части уравнения (2), задача Коши для этого уравнение имеет единственное решение, определенное на некотором интервале оси времени 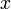, содержащем начальное значение 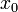(этот интервал, вообще говоря, может не совпадать со всей осью).

Основные задачи и результаты теории дифференциальных уравнений: существование и единственность решения различных задач дляОДУ, методы решения простейших ОДУ, качественное исследование решений ОДУ без нахождения их явного вида.

Примеры

§ Одно из простейших применений дифференциальных уравнений — решение нетривиальной задачи нахождения траектории тела по известным проекциям ускорения. Например, в соответствии со вторым законом Ньютона, ускорение тела пропорционально сумме действующих сил; соответствующее дифференциальное уравнение имеет вид 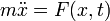. Зная действующие силы (правая часть), можно решить это уравнение и, учитывая начальные условия (координаты и скорость в начальный момент времени), найти траекторию движения точки.

§ Дифференциальное уравнение 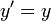, вместе с начальным условием , задаёт экспоненту: . Если 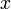обозначает время, то эта функция описывает рост популяции в условиях неограниченности ресурсов и многое другое.

§ Решением дифференциального уравнения 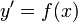, правая часть которого не зависит от неизвестной функции, является неопределённый интеграл: , где 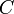— произвольная константа.

Дифференциальные уравнения первого порядка