Сумма степенного ряда. Дифференцирование и интегрирование степенных рядов
Пусть для степенного ряда
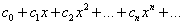 (29)
(29)
радиус сходимости R > 0, т.е. этот ряд сходится на интервале 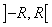 . Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f(x), можем записать равенство
. Тогда каждому значению х из интервала сходимости соответствует некоторая сумма ряда. Следовательно, сумма степенного ряда есть функция от х на интервале сходимости. Обозначая её через f(x), можем записать равенство
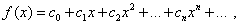 (30)
(30)
понимая его в том смысле, что сумма ряда в каждой точке х из интервала сходимости равна значению функции f(x) в этой точке. В этом же смысле будем говорить, что степенной ряд (29) сходится к функции f(x) на интервале сходимости. Вне интервала сходимости равенство (30) не имеет смысла.
Теорема 1.Степенной ряд (30) в интервале его сходимости можно почленно дифференцировать неограниченное число раз, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что исходный ряд, а суммы их соответственно равны 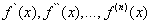 .
.
Теорема 2.Степенной ряд (30) можно неограниченное число раз почленно интегрировать в пределах от 0 до х, если 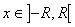 , причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
, причём получающиеся при этом степенные ряды имеют тот же радиус сходимости, что и исходный ряд, а суммы их соответственно равны
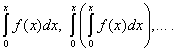
Дата добавления: 2016-07-18; просмотров: 3792;











