Интеграл с переменным верхним пределом
Рассмотрим функцию  , заданную на отрезке
, заданную на отрезке 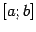 , и предположим, что она интегрируема на отрезке
, и предположим, что она интегрируема на отрезке 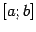 . Тогда при любом
. Тогда при любом 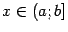 эта функция будет интегрируема на отрезке
эта функция будет интегрируема на отрезке  и, следовательно, функция
и, следовательно, функция
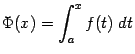
определена при всех 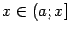 . При
. При 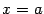 мы по определению положим её равной 0, то есть будем считать, что
мы по определению положим её равной 0, то есть будем считать, что 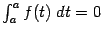 для любой функции
для любой функции 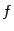 и точки
и точки 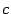 из её области определения. Итак, функция
из её области определения. Итак, функция 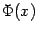 равняется значению определённого интеграла с переменным верхним пределом, вычисленного от интегрируемой функции
равняется значению определённого интеграла с переменным верхним пределом, вычисленного от интегрируемой функции  , не обязательно непрерывной.
, не обязательно непрерывной.
Теорема 3.11 Функция 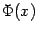 , определённая выше, непрерывна при всех
, определённая выше, непрерывна при всех 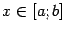 для любой интегрируемой функции
для любой интегрируемой функции 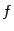 .
.
Доказательство. Заметим, что если функция  положительна, то значение
положительна, то значение 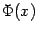 интерпретируется как площадь под графиком
интерпретируется как площадь под графиком 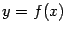 , лежащая над отрезком
, лежащая над отрезком  . Если дать
. Если дать 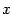 приращение
приращение 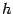 , то площадь получит приращение в виде площади полоски, лежащей над отрезком
, то площадь получит приращение в виде площади полоски, лежащей над отрезком 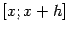 (см. рис.).
(см. рис.).
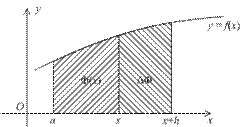
Рис.3.4.
Эта площадь, вследствие ограниченности интегрируемой функции, мала, если приращение 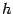 мало; это и означает непрерывность функции
мало; это и означает непрерывность функции 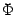 в точке
в точке 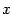 .
.
Проведём теперь более аккуратные рассуждения, не предполагая, что функция принимает положительные значения.
Пусть фиксирована точка 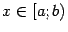 и взято такое приращение
и взято такое приращение 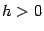 , что
, что 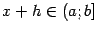 . Пользуясь аддитивностью интеграла, получаем, что
. Пользуясь аддитивностью интеграла, получаем, что
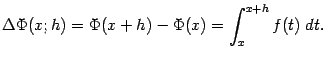
Согласно неравенству (3.5),
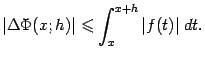
Но по теореме 3.5 функция  ограничена, поэтому существует такая постоянная
ограничена, поэтому существует такая постоянная 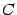 , что
, что 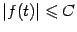 при всех
при всех 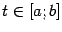 и, в том числе, при
и, в том числе, при 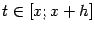 . Воспользовавшись теоремой об интегрировании неравенства, получаем, что
. Воспользовавшись теоремой об интегрировании неравенства, получаем, что
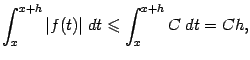
откуда
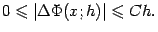
При 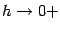 получаем по теореме "о двух милиционерах", что
получаем по теореме "о двух милиционерах", что 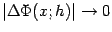 и
и 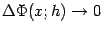 , что означает, что функция
, что означает, что функция 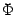 непрерывна справа в любой точке
непрерывна справа в любой точке 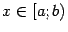 .
.
Рассматривая аналогично отрезок 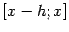 при
при 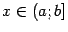 и
и 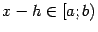 , получаем, что
, получаем, что
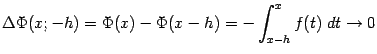
при 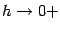 , что означает непрерывность функции
, что означает непрерывность функции 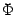 слева в любой точке
слева в любой точке 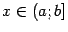 .
.
Тем самым функция 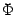 непрерывна справа в точке
непрерывна справа в точке 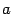 , непрерывна слева в точке
, непрерывна слева в точке 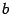 и непрерывна (с обеих сторон) в любой точке
и непрерывна (с обеих сторон) в любой точке 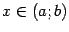 , что и требовалось доказать.
, что и требовалось доказать.
Теорема 3.12 Пусть функция  непрерывна на отрезке
непрерывна на отрезке 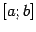 и функция
и функция 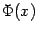 определена всё той же формулой. Тогда
определена всё той же формулой. Тогда 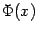 имеет производную в любой точке интервала
имеет производную в любой точке интервала 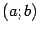 , производную справа в точке
, производную справа в точке 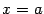 и производную слева в точке
и производную слева в точке 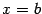 , причём эти производные совпадают со значением функции
, причём эти производные совпадают со значением функции  в соответствующей точке:
в соответствующей точке:
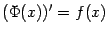 при
при 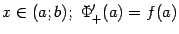 и
и 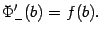
Доказательство. Снова рассмотрим приращение 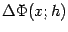 при
при 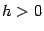 ,
, 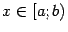 ,
, 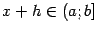 . Поскольку функция
. Поскольку функция  непрерывна, мы можем применить теорему о среднем к интегралу по отрезку
непрерывна, мы можем применить теорему о среднем к интегралу по отрезку 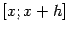 :
:
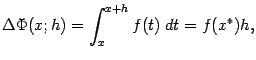
где 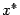 -- некоторая точка отрезка
-- некоторая точка отрезка 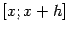 . Получаем, деля на
. Получаем, деля на 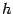 :
:
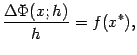
откуда при 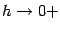 из непрерывности
из непрерывности  следует, что
следует, что
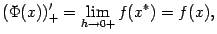
поскольку 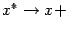 при
при 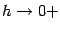 . Получили, что правая производная совпадает с
. Получили, что правая производная совпадает с  во всех точках
во всех точках 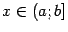 .
.
Аналогично доказывается, что левая производная 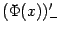 совпадает с
совпадает с  во всех точках
во всех точках 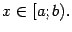 Во внутренних точках
Во внутренних точках 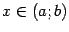 совпадение производных слева и справа со значением
совпадение производных слева и справа со значением  означает, что функция
означает, что функция 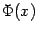 имеет производную
имеет производную 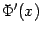 , равную
, равную  .
.
Точно так же доказывается, что производная интеграла
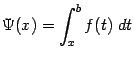
от непрерывной функции  по переменному нижнему пределу равняется
по переменному нижнему пределу равняется 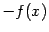 :
:
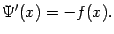
Равенство 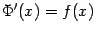 означает, что функция
означает, что функция 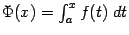 является первообразной для
является первообразной для  на интервале
на интервале 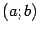 . Другая первообразная -- это, очевидно, функция
. Другая первообразная -- это, очевидно, функция 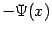 .
.
Итак, мы получили важный результат о наличии первообразной у любой непрерывной функции:
Теорема 3.13 Пусть  -- непрерывная на интервале
-- непрерывная на интервале 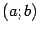 функция. Тогда на интервале
функция. Тогда на интервале 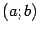 функция
функция  имеет некоторую первообразную
имеет некоторую первообразную 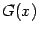 , то есть
, то есть 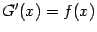 при всех
при всех 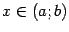 .
.
Доказательство. Для доказательства достаточно фиксировать произвольную точку 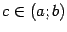 и положить
и положить
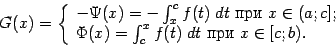
При  эти определения не противоречат друг другу, поскольку и та, и другая формулы дают
эти определения не противоречат друг другу, поскольку и та, и другая формулы дают 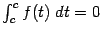 .
.
Нетрудно видеть, что при 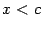 получается
получается 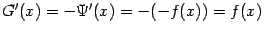 , при
, при 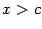 получаем
получаем 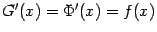 . При
. При  производная слева даёт значение
производная слева даёт значение 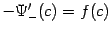 , а производная справа -- значение
, а производная справа -- значение 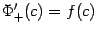 , так что производные слева и справа совпадают и
, так что производные слева и справа совпадают и 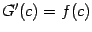 , что и завершает доказательство.
, что и завершает доказательство.
Пусть теперь 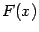 -- произвольная первообразная для непрерывной функции
-- произвольная первообразная для непрерывной функции  , заданной на некотором интервале
, заданной на некотором интервале 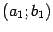 , содержащем отрезок
, содержащем отрезок 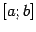 . Мы уже проверили, что функция
. Мы уже проверили, что функция 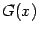 , такая что
, такая что 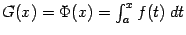 при
при 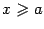 служит тогда первообразной для
служит тогда первообразной для 
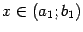 , а поскольку любые первообразные для одной и той же функции на заданном интервале могут отличаться лишь постоянным слагаемым, получаем, что
, а поскольку любые первообразные для одной и той же функции на заданном интервале могут отличаться лишь постоянным слагаемым, получаем, что
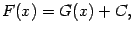
где 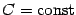 , при всех
, при всех 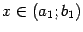 , в том числе и при
, в том числе и при 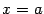 и
и 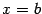 . Получаем
. Получаем 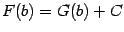 и
и 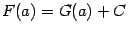 , откуда
, откуда
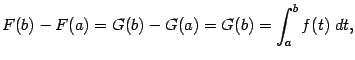
поскольку 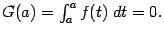 Итак, меняя обозначение переменной интегрирования на
Итак, меняя обозначение переменной интегрирования на 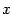 , получаем в итоге формулу
, получаем в итоге формулу
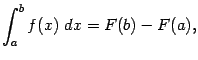
| (3.6) |
где 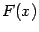 -- произвольная первообразная для функции
-- произвольная первообразная для функции  . Эта формула называется формулой Ньютона - Лейбница. Она играет ключевую роль в интегральном исчислении и во всём математическом анализе.
. Эта формула называется формулой Ньютона - Лейбница. Она играет ключевую роль в интегральном исчислении и во всём математическом анализе.
Напомним, что мы получили её в предположении, что функция  непрерывна. Если функция
непрерывна. Если функция  имеет разрыв на отрезке
имеет разрыв на отрезке 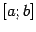 , то разность значений первообразной может не иметь никакого отношения к величине определённого интеграла. Поэтому при применении формулы Ньютона - Лейбница нужно строго следить за законностью этого действия.
, то разность значений первообразной может не иметь никакого отношения к величине определённого интеграла. Поэтому при применении формулы Ньютона - Лейбница нужно строго следить за законностью этого действия.
Смысл формулы Ньютона - Лейбница (3.6) состоит в том, что для нахождения определённого интеграла 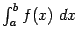 нам достаточно теперь найти произвольную первообразную
нам достаточно теперь найти произвольную первообразную 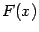 для функции
для функции  (напомним, что для этого надо найти неопределённый интеграл) и взять разность значений этой первообразной в концах отрезка,
(напомним, что для этого надо найти неопределённый интеграл) и взять разность значений этой первообразной в концах отрезка, 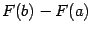 .
.
Итак, формула Ньютона - Лейбница устанавливает связь между определённым интегралом от данной функции и первообразной для этой функции, то есть между определённым и неопределённым интегралами. Заметим, что смысл этих двух понятий первоначально совершенно различен: неопределённый интеграл -- это набор функций (первообразных), а определённый интеграл -- это число (равное пределу интегральных сумм).
При вычислениях разность 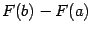 часто называют подстановкой в функцию
часто называют подстановкой в функцию 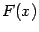 пределов
пределов 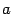 и
и 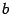 и обозначают
и обозначают 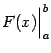 . Таким образом, по определению,
. Таким образом, по определению,
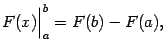
а формулу Ньютона - Лейбница можно записать в виде
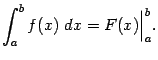
Пример 3.1 Для нахождения значения определённого интеграла
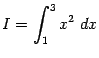
найдём первообразную для подынтегральной функции 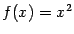 , вычислив неопределённый интеграл:
, вычислив неопределённый интеграл:
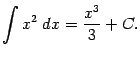
Поскольку нас интересует любая первообразная, то мы можем взять 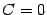 (с тем же успехом могли взять и
(с тем же успехом могли взять и 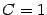 , и
, и 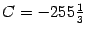 , и т. п., но вид первообразной при
, и т. п., но вид первообразной при 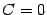 проще, а постоянные сласаемые всё равно взаимно уничтожатся при вычислении подстановки). Итак, берём
проще, а постоянные сласаемые всё равно взаимно уничтожатся при вычислении подстановки). Итак, берём 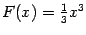 и вычисляем подстановку, беря в ней пределы равными пределам интегрирования:
и вычисляем подстановку, беря в ней пределы равными пределам интегрирования:
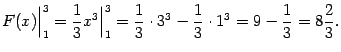
Получаем, что
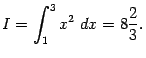
Пример 3.2 Найдём определённый интеграл
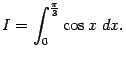
Поскольку
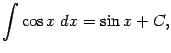
в качестве первообразной 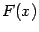 можно взять
можно взять 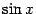 (положив
(положив 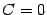 ). Поэтому
). Поэтому
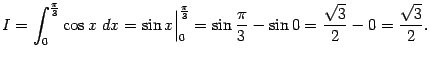
Дата добавления: 2016-07-18; просмотров: 3364;











