Множества и основные действия над множествами. Свойства действий над множествами.

П р и м е р ы. 1. Множество детей является подмножеством всего населения. 2. Пересечением множества целых чисел с множеством поло- жительных чисел является множество натуральных чисел. 3. Объединением множества рациональных чисел с множеством иррациональных чисел является множество действительных чисел.4. Нуль является дополнением множества натуральных чисел

относительно множества неотрицательных целых чисел.

Множество совокупность объектов, обладающих определенным свойством, объединенных в единое целое.. Пример:Множество действительных чисел, множество натуральных чисел, множество жителей данного города, множество деревьев на земле.

Среди множеств выделяют особое множество - пустое множество. Пустое множество-множество, не содержащее ни одного элемента.Пример:Множество всех действительных корней уравнения 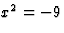пусто.

Множество считается определенным , если указаны все его элементы.Эти элементы могут быть указаны с помощью некоторого общего признака или с помощью некоторого списка, где обозначены все элементы.Последний способ возможен только в том случае, если множество имеет конечное число элементов.

Конечное множество-множество, состоящее из конечного числа элементов.

Комбинаторика есть теория конечных множеств.Поэтому далее будем иметь дело лишь с конечными множествами.Пример:Множество всех студентов факультета математики и информатики.Основной характеристикой конечного множества является число его элементов.Теория конечных множеств изучает правила: как, зная количество элементов некоторых множеств, вычислитьколичество элементов других множеств, которые составлены из первых с помощью некоторых операций.Бесконечное множество-непустое множество, не являющееся конечным.Пример:Множество натуральных чисел является бесконечным.

Упорядоченное множество

Множество, каждому элементу которого поставлено в соответствие некоторое число (немер этого элемента) от 1 до n, где n - число элементов множества, так что различным элементам соответствуют различные числа.

Каждое конечное множество можно сделать упорядоченным, если, например, переписать все элементы в некоторый список (a, b, c, d,...), а затемпоставить в соответствие каждому элементу номер места, нк котором он стоит в списке. Возможны различные способы задания множеств.Один из них состоит в том, что дается полный список элементов, входящих в это множество.

Итак, множества можно задавать двумя способами:

1. Перечислением элементов множества;

2. Описанием общего (характеристического) свойства, объединяющего элементы.

Множества А и В равны,если они состоят из одних и тех же элементов.

1. A=A(рефлексивность);
2. Если А=В, то В=А(симметричность);
3. Если А=В и В=С, то А=С(транзитивность).

Пример: Если А - множество всех действительных корней уравнения 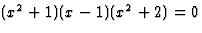- множество всех натуральных чисел меньших 2, то А=В={1}.

Заметим, что отношения равенства и включения имеют место не для всех множеств.