Рассмотрим участок 1 до сечения 1.
В опоре А действует сосредоточенная сила RA = 7,2 кН. На участке 1 поперечная сила остается постоянной: Q1 = Ra = 7,2 кН (рис. 31.3).

Изгибающий момент в точке А равен нулю, т. к. здесь нет момента внешней пары сил: МА = 0.
Момент в точке С (граница участка, z = 4м) МС = Ra * 4; Мс = 7,2 • 4 = 28,8кН • м.
Эпюра очерчивается прямой линией, наклонной к оси Oz (рис. 31.3).
Рассмотрим участок 2 (рис. 31.3). Здесь действует распределенная нагрузка интенсивностью q = 4кН/м. При перемещении вдоль оси балки направо распределенная нагрузка суммируется. Эпюра Q2 — прямая линия, наклонная к оси Oz. Распределенная нагрузка направлена вниз (см. Основные правила построения эпюр, п. 4), здесь эпюра изгибающего момента очерчена параболой, обращенной выпуклостью вверх.
Реакция в опоре Ra и распределенная нагрузка направлены в разные стороны. Следовательно, возможна точка, в которой, по правилу 2, Q2 = 0, а изгибающий момент экстремален.
Для построения эпюры моментов необходимо составить уравнение поперечной силы на участке 2 и приравнять величину поперечной силы нулю. Из уравнения можно определить координату точки, в которой изгибающий момент экстремален.
Проводим необходимые расчеты, определяем величины поперечных сил и изгибающих моментов в характерных точках.
Рассмотрим участок 2, сечение 2 (рис. 31.3).
Уравнение поперечной силы
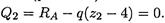
Откуда:
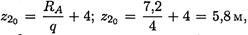
z20 — координата точки, где изгибающий момент экстремален, т. к. Q2 = 0.
Уравнение момента на участке 2:
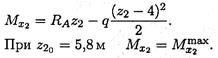
Максимальное значение изгибающего момента на участке 2
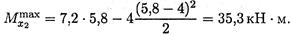
Значения поперечной силы и изгибающего момента в точке В: QB = RB = 16,8кН; МВ = 0.
Строим эпюру поперечной силы. Первый участок — прямая линия, параллельная оси Oz. В точке С эпюра становится наклонной. Строим эпюру изгибающих моментов (рис. 31.3).
Участок 1 эпюра — прямая линия; Ма = 0; Мс = 28,8 кН*м.
Участок 2 эпюра — парабола с экстремумом в точке z = 5,8 м; М z mах = 35,3кН*м; МВ = 0.
Пример 3. Построить эпюры Qy и Мх для балки, изображенной на рис. 2.51, а.
Решение

Из условия симметрии очевидно, что
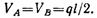
Проводим произвольное сечение I — I на расстоянии z от опоры А балки и рассматриваем левую отсеченную часть. Поперечная сила в произвольном сечении

— поперечная сила изменяется по линейному закону.
Найдем значение Qv в начале и в конце участка:
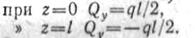
Эпюра Qy показана на рис. 2.51, б.
Изгибающий момент в произвольном сечении
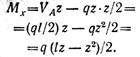
— изгибающий момент изменяется но закону квадратной параболы.
Вычислим Мк в начале, посередине и в конце участка:
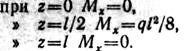
Эпюра Мх показана на рис. 2.51, е.
 Пример 4. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.54, а.
Пример 4. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.54, а.
Решение
Определим опорные реакции;
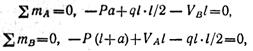
откуда
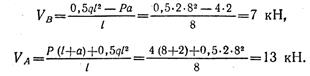
Составим проверочное уравнение:
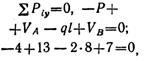
следовательно, реакции определены верно.
Балка имеет два участка I, II (рис. 2.54, а). На участке I при изменении z от 0 до 1 м Q Iy = — Р = — 4 кН постоянна; МxI = Рz = — 4z1 — прямая линия; при z = 0 МxI = 0; при z = 2 м МxI = — 4*2= — 8 кН-м.
Для сечения на участке II при изменении z от 2 до 10 м
Qlyl = — P+VA — q(z — 2) = — 4 + 13 — 2 (z — 2) — прямая линия;
Mx" = Pz + VA (z — 2) — 0,5q (z — 2)2 = — 4z + 13 (z — 2) — (z — 2)2 — парабола.
Найдем на участке II сечение, соответствующее экстремальному значению изгибающего момента: для этого приравняем нулю значение поперечной силы на этом участке:
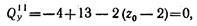
откуда z0 = 6,5 м.
Подставляя в уравнение для М11х найденное значение z0, получаем:
приz0 = 6,5 м М11х = Мтах = 12,25 кН-м; кроме того, при z = 2 м М11х = 8 кН-м, Qlly = 9 кН; при z = 10 м М11х = 0, Qv = — 7 кН. По этим значениям построены эпюры поперечных сил и изгибающих моментов (рис. 2.54, б, в).

Пример 5. Построить эпюры изгибающих моментов и поперечных сил для балки, изображенной на рис. 2.55, а.
Решение
 |
Определяем опорные реакции:
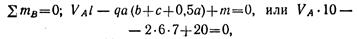
Откуда
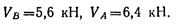
Составляем проверочное уравнение:
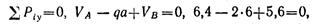
следовательно, опорные реакции определены верно.
Балка имеет три участка I, II, III (рис. 2.55, а): участок I — z = 0 — 6 м; участок II — z = 6 — 8 м; участок III – 2 = 8 — 10 м.
На участке I при изменении z от 0 до 6 м
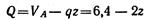 -- уравнение прямой линии, наклоненной к оси балки;
-- уравнение прямой линии, наклоненной к оси балки;
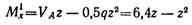 -- уравнение параболы.
-- уравнение параболы.
На участке II при изменении z от 6 до 8 м
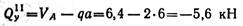 -- уравнение прямой, параллельной оси балки;
-- уравнение прямой, параллельной оси балки;
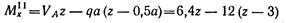 -- уравнение прямой, наклоненной к оси балки.
-- уравнение прямой, наклоненной к оси балки.
На участке III при изменении z от 8 до 10 м
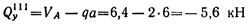 -- уравнение прямой (такой же, как и для участка II);
-- уравнение прямой (такой же, как и для участка II);
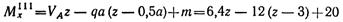 -- уравнение прямой, наклоненной к оси балки.
-- уравнение прямой, наклоненной к оси балки.
Подставляя в уравнения поперечных сил и изгибающих моментов значения абсцисс z, соответствующие границам участков, получаем величины Qy и Мх в соответствующих сечениях:
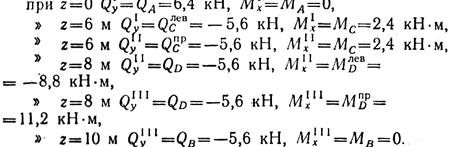
В сечении, где приложена сосредоточенная пара сил, имеется скачок в эпюре изгибающих моментов, равный величине момента пары т = 20 кН-м. Чтобы найти максимальное значение изгибающего момента на участке I, приравняем нулю значение поперечной силы на этом участке:
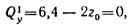
откуда z0 = 3,2 м.
Подставив это значение г0 в уравнение для MlX, получаем:
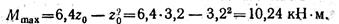
Следует иметь в виду, что наибольший изгибающий момент может не совпадать с аналитическим максимумом, как, в частности, оказалось в нашем случае.
Эпюры поперечных сил и изгибающих моментов построены на рис. 2.55,б, в.
Заметим, что при определении изгибающих моментов на участке III проще было рассматривать равновесие правой отсеченной части балки.
Пример 6. Построить эпюры поперечных сил и изгибающих моментов для балки, изображенной на рис. 2.56, а.
 |
Решение
Определим опорные реакции:
откуда 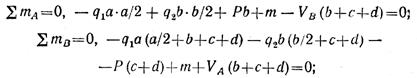
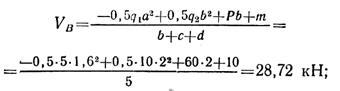
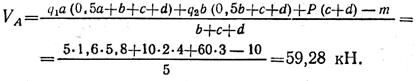
Составим проверочное уравнение:
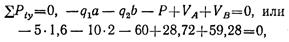
следовательно, реакции вычислены верно.
Балка имеет четыре участка I, II, III, IV (рис. 2.56, а).
Проводим сечение в пределах участка I (0 ≤ z ≤ 1,6 м) и, рассматривая равновесие левой отсеченной части, определяем аналитические выражения поперечной силы и изгибающегомомента на этом участке:
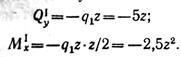
Поперечная сила изменяетсяпо линейному закону:
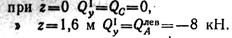
Изгибающий момент М1Х изменяется по закону квадратной параболы, параболу строим по двум точкам:
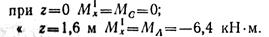
Аналогично, проводя сечения на участке II (1,6 м ≤ z ≤ 3,6 м) и рассматривая равновесие левой отсеченной части балки, получаем:
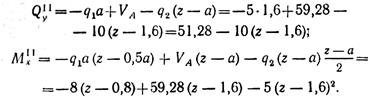
Поперечная сила на участке II, как и на участке I, изменяется по линейному закону:
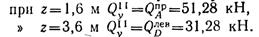
Изгибающий момент на участке II изменяется по закону квадратной параболы:
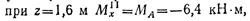
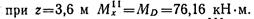
Проводим сечение на участке III и рассматриваем равновесие правой части, отсчитывая абсциссы от точки В (1,8 м < z1 < 3 м).
К правой отсеченной части балки приложено меньше внешних сил, чем к левой, поэтому составление аналитических выражений для поперечной силы и изгибающего момента будет проще:
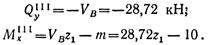
Поперечная сила на участке III постоянна. Изгибающий момент изменяется по линейному закону:
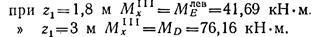
Проводя сечение на участке IV, так же рассматриваем равновесие правой отсеченной части (0 ≤ z1 < 1,8 м):
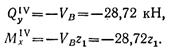
Эпюра поперечных сил изображается прямой, параллельной оси балки, как и на третьем участке. Эпюра изгибающих моментов имеет вид наклонной прямой:
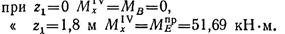
По полученным данным на рис. 2.56, б, в построены эпюры поперечных сил и изгибающих моментов.
Контрольные вопросы и задания
1. Если эпюра поперечной силы ограничена наклонной прямой, как выглядит эпюра изгибающего момента?
2. Как определить положение экстремального значения изгибающего момента при действии распределенной нагрузки на участке балки?
3. Распределенная нагрузка направлена вверх. Как выглядит парабола, очерчивающая эпюру изгибающих моментов вдоль оси бруса?
4. Определите координату z, в которой поперечная сила равна нулю (рис. 31.4).
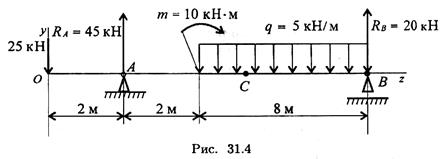
5. Определите величину изгибающего момента в точке С (z = = 5 м), используя схему рис. 31.4.
ЛЕКЦИЯ 32
Дата добавления: 2020-08-31; просмотров: 870;











