Примеры решения задач. Проверить жесткость двутавровой балки

Пример 1. Проверить жесткость двутавровой балки (рис. 33.7). Принять

Сечение балки — двутавр № 45.

Решение

Используем принцип независимости действия сил. По приведен­ным в таблице формулам рассчитываем прогиб балки в точке от каждого вида нагружения отдельно (рис. 33.7 (1, 2, 3)).

Поскольку все действующие нагрузки прогибают балку вниз, результаты дей­ствия нагрузок можно сложить. Получен­ный суммарный прогиб сравним с допус­каемым прогибом.

Допускаемый прогиб

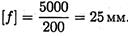
Суммарный прогиб

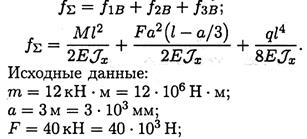
q = 4кН/ м = 4Н/мм; l = 5м = 5-10³мм.

Для двутавра № 45 ГОСТ 8239-89

J_x = 27696 см⁴ = 27,7 • 10⁷мм⁴.

Тогда

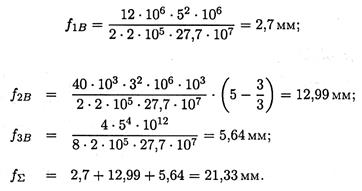
21,33 < 25 — условие жесткости выполняется.

Максимальный прогиб не превышает допускаемого значения.

Пример 2. Определить угол поворота и прогиб свободного конца консольной балки, изображенной на рис. 2.61.

Решение

Поместим начало координат на левом конце балки и составим обобщенные уравнения упругой линии и углов поворота:

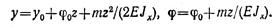
Определяем начальные параметры у₀ и ф₀ исходя из условий опорных закреплений:

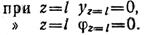
Из второго условия находим φ₀:

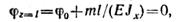откуда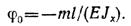

Знак минус перед значением угла поворота показы­вает, что поворот начального сечения происходит по ча­совой стрелке. Из второго условия находим у₀:

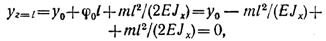
Откуда

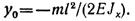
Знак минус перед значением прогиба показывает, что он направлен вниз, противоположно положительному на­правлению оси у.

Пример 3. Определить прогиб посередине пролета балки, нагруженной равномерно распределенной нагруз­кой (см. рис. 2.51, а).

Решение

Поместим начало координат на левой опоре балки и составим обобщенные уравнения упругой линии и углов поворота:

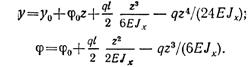
Определяем начальные параметры y₀ и φ₀ исходя из условия опорных закреплений:

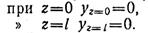
Из первого условия находим у₀ = 0.

Из второго условия определяем φ₀:

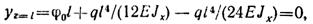
Откуда

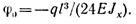
Подставляя у₀ и φ₀ в уравнение прогибов, получаем

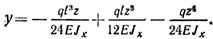
В середине пролета при z = 0,5l прогиб принимает максимальное значение

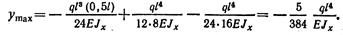
Знак минус перед значением прогиба показывает, что он направлен вниз, т. е, в сторону, противоположную по­ложительному направлению оси у.

Пример 4. Для балки, изображенной на рис. 2.62, опре­делить прогиб под точкой при­ложения силы и углы поворота на опорах А и В.

Решение

Поместим начало координат на опоре A. Раз­обьем балку на два участка и составим обобщенные уравне­ния упругой линии и углов по­ворота для каждого из них, предварительно определив опорные реакции:

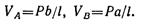
для первого участка

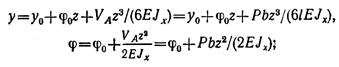
для второго участка

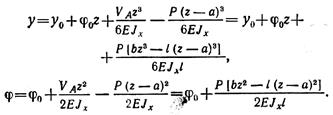
Определяем начальные параметры исходя из условий опорных закреплений:

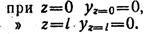
Из первого уравнения находим у₀:

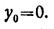
Из уравнения прогибов для второго участка находим угол поворота φ₀ сечения на левой опоре:

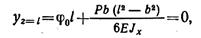
Откуда

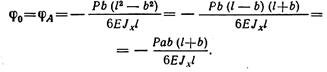
Подставив значение φ₀ в уравнение прогибов первого участка, получим

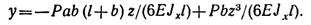
При z = a найдем прогиб сечения под точкой прило­жения силы Р:

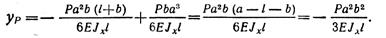
Используя уравнение углов поворота для второго участка

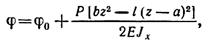
найдем при z = l угол поворота сечения на правой опоре В:

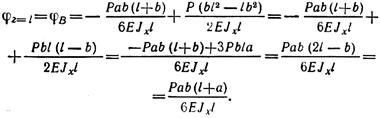
Угол поворота φ_В положителен, следовательно, он в отличие от угла поворота φ_А направлен против часовой стрелки.

При приложении силы Р посередине пролета балки, т. е. при а = b = l/2, углы поворота опорных сечений и про­гиб под точкой приложения силы примут значения:

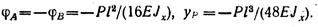
Пример 5. Определить максимальный прогиб двухопорной балки, нагруженной равномерно распределенной по всему пролету нагрузкой интенсивностью q и сосредоточенной силой Р посередине пролета.

Решение

Наибольший прогиб при симметричном нагружёный балки возникает посередине пролета, под точ­кой приложения силы Р. Этот прогиб может быть найден на основе принципа независимости действия сил как сумма прогибов от распределенной нагрузки интенсивностью q и сосредоточенной силы Р:

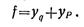
Составляющие части полного прогиба были вычислены в предыдущих примерах. Подставляя их значения, полу­чаем

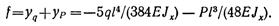
Оба составляющих прогиба направлены вниз и входят поэтому со знаком минус.