Вероятность попадания случайной величины на заданный участок.

Пусть случайная величина X распределена равномерно на интервале от a до b, причем плотность вероятности ее известна и равна f(x)=1/(b-a). Требуется определить вероятность попадания ее на участок от c до d (рис.9),т.е. .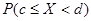

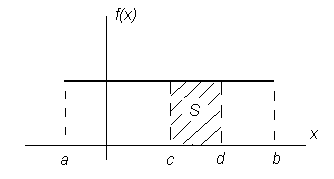
Рисунок 9 Определение вероятности попадания случайной величины на заданный участок

Определяя эту вероятность как интеграл от плотности вероятности f(x), получаем

.

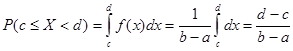Следовательно, вероятность попадания случайной величины на заданный участок от c до d определяется как площадь заштрихованного прямоугольника.

Округление результатов измерений имеет равномерное распределение.

Теорема Чебышева.

При достаточно большом числе независимых опытов среднее арифметическое из опытных данных сходится по вероятности к математическому ожиданию случайной величины.

Пусть a – истинное значение измеряемой величины, 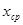- среднее арифметическое ряда измерений, 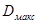- максимальное значение квадрата отклонения в произведенных измерениях, n – число измерений. Теорема Чебышева утверждает, что

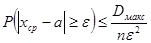. (5.1)

Для доказательства теоремы обратим внимание на то, что математическое ожидание любого измерения 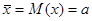, где a – неизвестное истинное значение измеряемой величины. Далее, так как

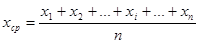, то

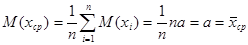, т.е. математическое ожидание среднего значения случайной величины также равно истинному значению a. Дисперсия величины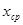

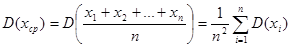. Так как можно написать, что

.

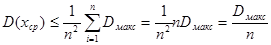Теперь после замены x на 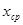и 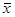на a легко получаем теорему Чебышева.

Из теоремы следует, что при любых конечных 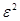и 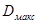будет справедливо предельное соотношение

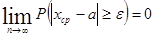или эквивалентное ему соотношение

.

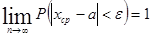Таким образом, теорема Чебышева доказывает, что среднее арифметическое опытных данных (измерений) мало отличается от истинного значения при большом числе испытаний. Однако входящее в неравенство значение 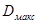указывает на то, что увеличением числа измерений нельзя полностью компенсировать ошибки измерительного инструмента.

Выводы теоремы можно распространить и на другие моменты распределения. Например, для дисперсии получаем приближенную формулу, пригодную для практических вычислений:

,

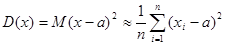где вместо a, согласно теореме Чебышева, можно пользоваться :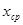

.

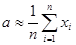Неравенство и теорема Чебышева для практических задач могут использоваться в тех случаях, когда известна дисперсия, очевидно, она должна быть конечной величиной.

Теорема Бернулли.

При достаточно большом числе независимых опытов n частота события A сходится по вероятности к вероятности этого события, т.е.

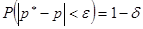, (5.2)

где 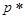- частота события A;

p – вероятность появления события A;

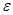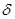, - сколь угодно малые положительные числа.

Пусть производится n независимых опытов, в каждом из которых событие A может произойти с вероятностью p. В результате этих опытов можно сформировать ряд, состоящий из случайных величин - чисел появлений интересующего нас события в каждом из n опытов:

.

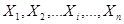Поскольку частота события A 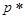представляет собой среднее арифметическое случайных величин 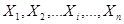и равно

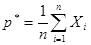, то математическое ожидание частоты события можно определить как

.

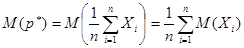Считая математические ожидания случайных величин 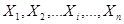одинаковыми и равными 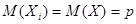, математическое ожидание частоты события будет равно

.

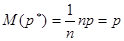Что и следовало доказать.

Пользуясь теоремой Бернулли в виде формулы (5.2) можно определить:

вероятность того, что при n испытаниях отклонение частоты события от вероятности не превзойдет величину ;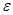

число испытаний n, необходимое для того, чтобы отклонение вероятности от частоты события не превышало 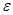при заданной вероятности P;

отклонение 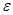частоты события от вероятности при данном числе испытаний n и заданной вероятности P.

Величину 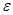называют «доверительным интервалом», а вероятность P – «надежностью» или «доверительной вероятностью».