Численное интегрирование

 

При вычислении определенных интегралов с помощью формулы Ньютона-Лейбница
b
! f(x)dx = F(b) - F(a) (6.1)

а

необходимо для подынтегральной функции f(x) найти первообразную F(x). Однако далеко не всякая подынтегральная функция f(x) имеет в качестве первообразной элементарную функцию.

Если интеграл не выражается через элементарные функции, то для его вычисления используют численные методы. Приведём примеры интегралов «не берущихся в конечном виде» :

, , , .

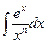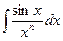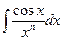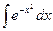Численные методы интегрирования применяют и тогда, когда аналитические методы интегрирования не приме­нимы или слишком сложны.

Например, если необходимо вычислить определенный интеграл от таблично заданной функции, то применение численно­го интегрирования является неизбежным.

Формулы для приближенного вычисления интегралов часто, называют квадратурными.

6.1. Квадратурные формулы Ньютона-Котеса

(Котес Роджер (10. 7.1682–5.6.1716) – английский математик, друг и ученик И. Ньютона)

Пусть требуется вычислить определенный интеграл

b
! y(x)dx = F(b) - F(a) (6.2)

а

При выводе квадратурных формул для приближенно­го вычисления определенного интеграла вспомним его геометрический смысл – интеграл равен площади кри­волинейной трапеции, ограниченной графиком подынтег­ральной функции, осью Ох и отрезками прямых х = a и х = b.

Разобьем отрезок [а, b] на п частей точками хi:
xi = a + ih, i = 0, 1,..., n; x0 = a, xn = b, 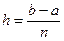(6.3)

Обозначим через yi значения функции в точках xi. За­меним подынтегральную функцию интерполяционным многочленом Лагранжа (4.17):

y(x) = Ln(x) = 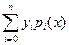= 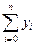× 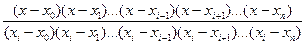(6.4)

Тогда получим приближенную формулу для вычисле­ния интеграла:

 

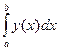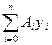» , (6.5)

где Ai – числовые коэффициенты, которые не зависят от подынтегральной функции и их значения для заданного п всегда можно опреде­лить.

Выведем формулы для вычисления коэффициентов Ai. Введем обозначения

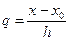, q[n + 1] = q(q - l)...(q - n). Тогда многочлен Лагранжа можно записать в виде

Ln(x) = ,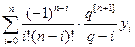

Заменяя под знаком интеграла в (6.5) функцию у(х) многочленом Ln(x),

получим

= ,

 

= .

 

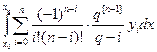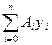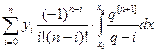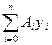Отсюда следуют формулы для вычисления коэффици­ентов Ai:

Ai = 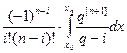= = 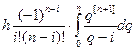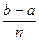· 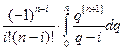= (b – a)Hi,

где i = 0, 1,..., n.

Коэффициенты Hi называются коэффициентами Котеca ивычисляются по формулам

Hi = 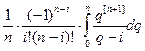, i = 0, 1,..., n. (6.6)

Далее рассмотрим простейшие квадратурные форму­лы, являющиеся частными случаями этих соотношений.

a) Формула прямоугольников

Формулы прямоугольников получаются заменой по­дынтегральной функции постоянным значением. В каче­стве такого значения выбирают значение функции в од­ной из точек отрезка [а, b]или на левом конце отрезка, или на правом конце, или в середине отрезка (рис. 6.1):

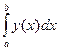» y(a)(b – a), (6.7)

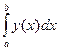» y(b)(b – a), (6.8)

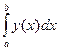» y( 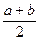)(b – a), (6.9)

 

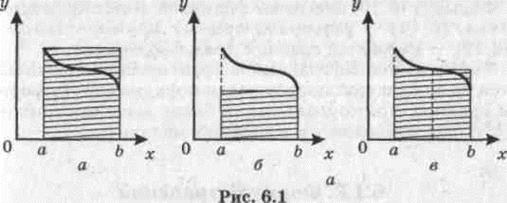
Если формулы (6.7)–(6.9) применить к каждой части [xi, xi + 1]частичного отрезка [а, b],получим общие формулы прямоу­гольников.Фактически, определенный интеграл в этом случае прибли­женно заменяется интегральной суммой:

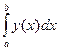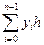» , (6.10)

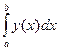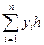» , (6.11)

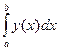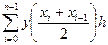» , (6.12)

Геометрически это означает, что площадь криволиней­ной трапеции приближенно заменяется площадью сту­пенчатой фигуры. В частности, рис. 6.2 иллюстрирует формулу (6.10).

 

 

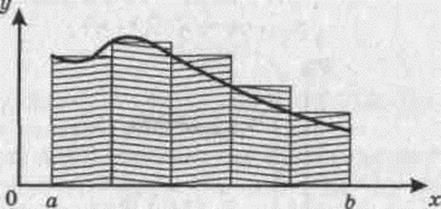
Рис. 6.2.

Формулу (6.10) называют формулой левых прямоуголь­ников, (6.11) – формулой правых прямоугольников, а (6.12) – формулой средних прямоугольников.

Формулы прямоугольников практически не использу­ются из-за большой погрешности порядка O(h) (у форму­лы средних прямоугольников более высокий порядок O(h2)).

б) Формула трапеций

Положим в формуле (6.6) п = 1 и вычислим значения Hi:

Hi = 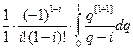, i = 0, 1;

H0 = = = = ;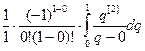

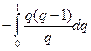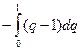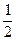H1 = 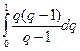= 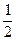, откуда A0 = A1 = .

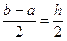Таким образом, заменяя подынтегральную функцию многочле­ном Лагранжа первой степени получаем формулу тра­пеций:

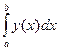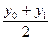» h, h = b – a. (6.13)

Геометрический смысл формулы трапеций (6.13) зак­лючается в том, что кривая у = у(х) заменяется отрезком прямой, проходящей через точки (х0, у0) и (х1, у1), или, в других обозначениях, (а, у(а)) и (b, у(b)) (рис. 6.3).

 
 

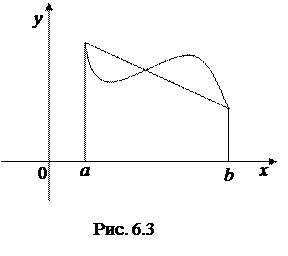Понятно, что формулы трапеций и средних прямоу­гольников являются точными для линейной функции.

Если обобщить (6.13) для равномерного разбиения от­резка на п частей, приходим к общей формуле трапеций (рис. 6.4):

 

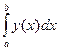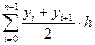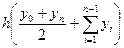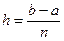» = , . (6.14)

 

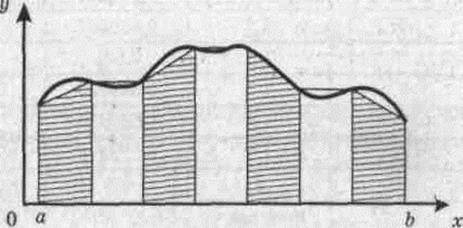
Рис. 6.4

Погрешность формулы трапеций (6.13) есть величина порядка O(h3). В этом можно убедиться, используя фор­мулу погрешности интерполяционного многочлена Лаг­ранжа. А для общей формулы трапеций (6.14) погреш­ность есть величина порядка O(h2), так как при суммировании погрешности накапливаются.

в) Формула Симпсона

(Симпсон Томас(20.8.1710–14.5.1751) – английский математик)

Применяя интерполяционную формулу Лагранжа при п = 2, получим значения коэффициентов:

Hi = 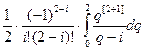, i = 0, 1, 2.

H0 = = ,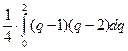

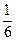H1 = - = ,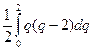

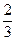H2 = = ,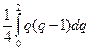

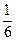h = 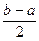, Ai = (b – a)Hi = 2hHi, A0 = 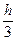, A1 = 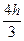, A2 = .

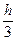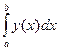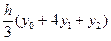» . (6.15)

Геометрический смысл формулы Симпсона (6.15) зак­лючается в том, что кривая у = у(х) заменяется частью параболы, проходящей через три точки (х0, у0), (х1, у1) и (х2, у2) (рис. 6.5, а).

Формула Симпсона точна не только для полинома вто­рой степени, но и для полинома третьей степени в силу симметрии, показанной на рис. 6.5, б.

 
 

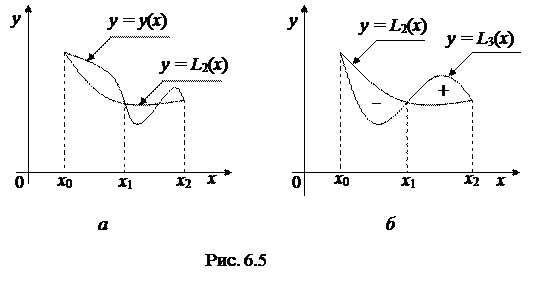Остаточный член формулы (6.15) имеет порядок O(h5). Общая формула Симпсона строится для четного п = 2m; при этом формула (6.15) применяется для каждо­го отрезков [х0, х2], [х2, х4], ... , [хп - 2, xn]:

 

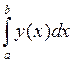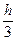» (у0 + 4у1 + 2у2 + 4у3 +...+2у2m-2 + 4y2т-1 + у2т) =

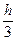
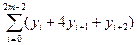= (6.16)

Остаточный член общей формулы Симпсона (6.16) имеет порядок O(h4).

г) Формулы Ньютона–Котеса высших порядков

Полагая в формуле (6.6) п = 3, можно вычислить зна­чения коэффициентов Ai:

A0 = 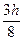, A1 = A2 = 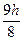, A3 = .

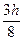и получить квадратурную формулу Ньютона

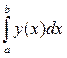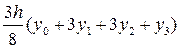» . (6.17)

Формула (6.17) имеет погрешность того же порядка, что и формула Симпсона (6.15), т. е. O(h5).

Приведем таблицу значений коэффициентов Котеса (табл. 1).

Таблица 1

п Но Н1 H2 Hз H4 H5 H6 Множи­тель для полу­чения Аi
1/2 1/2           h
1/6 4/6 1/6         2h
1/8 3/8 3/8 1/8       3h

 

Окончание табл. 1

п Но Н1 H2 Hз H4 H5 H6 Множи­тель для полу­чения Аi
7/90 32/90 12/90 32/90 7/90     4h
19/288 75/288 50/288 50/288 75/288 19/288   5h
41/840 216/840 27/840 272/840 27/840 216/840 41/840 6h

 

Например, квадратурная формула Ньютона–Котеса для п = 5 имеет вид

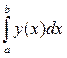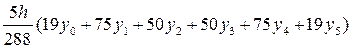» . (6.18)

Квадратурные формулы с нечетным числом узлов (п = 2, 4, 6) являются более удобными, т. е. выгоднее при­менять формулу Симпсона (6.15), чем формулу Ньютона (6.17), так как при одном и том же порядке погрешности формула Ньютона требует больше узлов (и больше вычис­лений), чем формула Симпсона. Аналогично, формула для п = 4 лучше, чем формула для п = 5, и т. д.

6.2. Правило Рунге оценки погрешности

Приведем сводку квадратурных формул с остаточны­ми членами.

Формула трапеций:

» .

 

» .

 

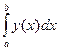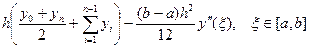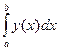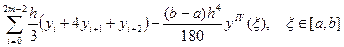Рассмотрим на примере общей формулы Симпсона (6.16) правило Рунге для оценки погрешности. Пусть подынтегральная функция четырежды непрерывно дифференцируема. Тогда формула остаточного члена имеет вид

R(h) = 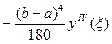(6.19)

 

где ξ – некоторое число из отрезка [а, b].

Предположим, что производная yIV(x) изменяется на этом отрезке медленно, и приближенно можно записать остаточный член в виде R(h) = Мh4, где М – постоянная. Пусть Sh, и S2h, соответственно значения интеграла, полу­ченные по общей формуле Симпсона с шагом h и 2h. Тог­да справедливы соотношения

= , = .

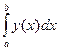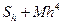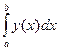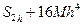Отсюда получим формулу для оценки погрешности

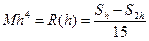(6.20)

Уточненное значение интеграла по формуле Симпсона вычисляется с учетом поправки

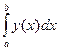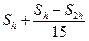= (6.21)

Для формулы трапеций также можно применить пра­вило Рунге. Так как формула остаточного члена общей формулы трапеций может быть представлена в виде R(h) = Mh2, справедливы соотношения

= , = .

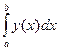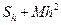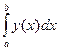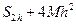Отсюда получим формулу для оценки погрешности:

Mh2 = R(h) = .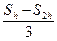

Теперь для интеграла можно записать (по правилу Рунге) формулу трапеций с поправкой

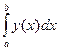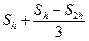= (6.22)

Замечание. Здесь необходимо подчеркнуть, что описанное правило Рунге применимо только тогда, когда выполняются указанные выше условия для функции у(х) – существование производной соответствующего порядка и ее ограниченность, точнее говоря, возможность приближенного представления по­грешности в виде R(h) = Mh4 для формулы Симпсона (R(h) = Mh2 для формулы трапеций), где М – постоянная. Погрешность представления остаточного члена в указанном виде считается достаточно малой. Эти условия для конкретной функции могут не выполняться, тогда правило Рунге не будет гарантировать приемлемый результат.
<== предыдущая лекция | следующая лекция ==>
Численное дифференцирование | Численные методы решения обыкновенных дифференциальных уравнений

Дата добавления: 2020-08-31; просмотров: 471;

Поиск по сайту:

Воспользовавшись поиском можно найти нужную информацию на сайте.

Поделитесь с друзьями:

Считаете данную информацию полезной, тогда расскажите друзьям в соц. сетях.
Poznayka.org - Познайка.Орг - 2016-2024 год. Материал предоставляется для ознакомительных и учебных целей.
Генерация страницы за: 0.024 сек.