Численные методы решения обыкновенных дифференциальных уравнений

Уравнение

F(x, у, у', у", ... , у⁽ⁿ⁾)= 0,

связывающее неизвестную функцию у(х),независимую переменную х и производные у'(x), у"(x),..., у⁽ⁿ⁾(x) неизвестной функции, называется обыкновенным дифференциальным уравнением. Порядок п старшей производной называется порядком дифференциального уравнения.

В задаче Коши для дифференциального уравнения п-го порядкаискомая функция у(х),кроме самого дифференциального уравнения, должна удовлетворять начальным условиям

у(х₀) = α₀, у'(х₀)= α₁, у"(х₀) = α₂,..., у⁽ⁿ^-1)(x₀) = α_n_-1.

Методы решения задач для дифференциальных уравнений можно разбить на три типа: точные, приближенные и численные.

Точныминазывают методы, с помощью которых решение дифференциального уравнения можно выразить через известные функции (элементарные функции или интегралы от элементарных функций). Точные методы решения известны только для некоторых классов дифференциальных уравнений (линейные дифференциальные уравнения, уравнения с разделяющимися переменными и др.).

Приближенными называют методы, в которых решение находят как предел последовательности функций, являющихся элементарными или интегралами от элементарных функций. Например, метод разложения искомой функции в ряд Тейлора является приближенным методом.

Численный метод решения дифференциального уравнения – алгоритм вычисления значений искомого решения у(х) на некотором дискретном множестве значений аргумента х. При этом вычисляемые значения искомого решения у(х) являются приближенными, но могут быть и точными.

7.1. Задача Коши

Рассмотрим задачу Коши для обыкновенного дифференциального уравнения первого порядка

y'(х) = f(x, у), (7.1)

y(x₀) = y₀ (7.2)

Требуется найти функцию у = у(х), которая удовлетворяет уравнению (7.1) на интервале (х₀, X) и начальному условию (7.2) в точке х₀.

Приведем без доказательства теорему существования и единственности решения задачи Коши.

Теорема 7.1. Пусть в области R{(x, у), |х - х₀| £ а, |у - у₀| £ b} функция f(x, у) непрерывна. Тогда на некотором отрезке |х - x₀| £ d существует решение уравнения (7.1), удовлетворяющее условию (7.2).

Если в области R функция f(x, у) удовлетворяет условию Липшица

| f(x, у₁) - f(x, y₂)| £ k | y₁ - у₂|, k > 0, k = const,

то указанное решение единственно.

Произведем разбиение отрезка [х₀, X] на п частей:

x_i = x₀ + ih, 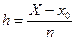. (7.3)

Найдем приближенные значения решения у(х) в точках x_i , i = 1, 2,..., n.

7.2. Метод Эйлера (ломаных)

Рассмотрим уравнение (7.1) в точках x_i, i = 0, 1, ... , n - 1 и заменим производную y'(x_i) разностной формулой

y'(x_i) = 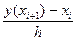(7.4)

Тогда получим рекуррентную формулу метода Эйлера для вычисления приближенных значений у(x_i ₊ ₁):

y_i_{+ 1}= y_i + h f(х_i, у_i), i = 0, 1,..., п - 1. (7.5)

Здесь через y_i обозначены приближенные значения y(x_i), т. е. у_i = у (x_i), i = 1, 2, ... , п.

На рис. 7.1 дана геометрическая иллюстрация метода Эйлера (7.5). Уравнение касательной к графику решения у(х) в точке (х₀, у₀) имеет вид

y = y₀ + f(x₀, y₀)(x – x₀) (7.6)

так как у'(х₀) = f(x₀, y₀). Интегральная кривая у(х) на отрезке [х₀, х₁] заменяется отрезком касательной (7.6), соединяющей точку (х₀, у₀) с точкой (х₁, у₁), где у₁ = у₀ + f(x₀, у₀)(х - х₀) (рис. 7.1). Точка (х₁, у₁) уже не лежит на интегральной кривой у = у(х), удовлетворяющей начальному условию (7.2).

При i = 1 формула (7.5) дает точку (х₂, у₂), которая определяется с помощью касательной у = y₁+ f(x₁, у₁)(х - x₁), проведенной в точке (х₁, у₁) к интегральной кривой у(х),

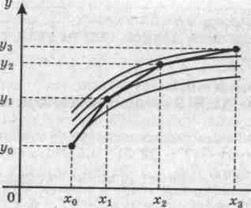
Рис. 7.1

удовлетворяющей уравнению (7.1) и начальному условию y(x₁) = y₁.

Таким образом, с каждым шагом i метод Эйлера (7.5) дает точки (x_i, y_i), которые, вообще говоря, удаляются от интегральной кривой, соответствующей точному решению задачи Коши (7.1), (7.2). Вместо интегральной кривой метод Эйлера дает ломаную, изображенную на рис. 7.1, поэтому его часто называют методом ломаных.

Формулу (7.5) можно получить и другим способом. Рассмотрим разложение искомого решения у(х) в ряд Тейлора в окрестности точки х₀:

у(х) = у(х₀) + у^¢(х₀)(х - х₀) + + ... .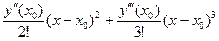

Ограничившись двумя слагаемыми и учитывая, что y'(х₀) = f(x₀, у₀), при х = х₁ получим (7.5).

Также здесь получен следующий результат – погрешность вычисления значения у₁ есть величина порядка O(h²), а погрешность значения у_п – величина порядка O(h). Из-за большой погрешности метод Эйлера применяется редко.

7.3. Метод Эйлера с уточнением

Для повышения точности метода Эйлера применяют следующий прием. Сначала находят приближенное значение решения по методу Эйлера:

,

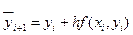а затем уточняют его по формуле

.

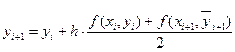Этот метод называется методом Эйлера-Коши, и рекуррентные соотношения для его реализации могут быть записаны в виде

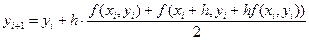, (7.7)

i = 0, 1, ..., n - 1

Метод Эйлера-Коши имеет погрешность порядка O(h²). Геометрическая иллюстрация метода Эйлера-Коши показана на рис. 7.2. Очередное приближение метода Эйлера-Коши соответствует точке пересечения диагоналей параллелограмма, построенного на двух звеньях ломаной метода Эйлера.

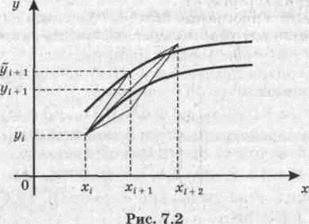
Метод Эйлера-Коши является одним из частных случаев методов Рунге-Кутта.

7.4. Методы Рунге-Кутта

Рассмотрим наиболее популярный метод решения задачи Коши – метод Рунге-Кутта. Этот метод позволяет строить формулы расчета приближенного решения практически любого порядка точности.

Выведем формулы метода Рунге-Кутта второго порядка точности. Для этого решение представим куском ряда Тейлора, отбрасывая члены с порядком выше второго. Тогда приближенное значение искомой функции в точке x_i, можно записать в виде:

y₁ = у(х₀) + у^¢(х₀)(х - х₀) + 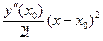= y₀ + f(x₀, y₀)h + 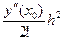. (7.8)

Вторую производную у"(х₀) можно выразить через производную функции f(x, у), однако в методе Рунге-Кутта вместо производной используют разность

,

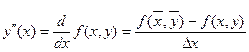соответственно подбирая значения параметров , , 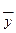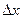. Тогда (7.8) можно переписать в виде

y₁ = y₀ + h[bf(x₀, y₀) + αf(x₀ + γh, y₀ + δh)], (7.9)

где α, β, γ и δ – некоторые параметры.

Рассматривая правую часть (7.9) как функцию аргумента h, разложим ее по степеням h:

y₁ = y₀ + (α + β)hf(x₀, y₀) + αh²[γ f_x(x₀, y₀) + δf(x₀, y₀)],

и выберем параметры α, β, γ и δ так, чтобы это разложение было близко к (7.8). Отсюда следует, что

α + β = 1, αγ = 0,5, αδ = 0,5 f(х₀, y₀).

С помощью этих уравнений выразим β, γ и δ через параметр α, получим

y₁ = y₀ + h[(1 – α) f(x₀, y₀) + αf(x₀ + 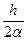, y₀ + 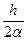f(x₀, y₀))],

0 < α £ 1. (7.10)

Теперь, если вместо (х₀, у₀)в (7.10) подставить (х₁, у₁),получим формулу для вычисления у₂– приближенного значения искомой функции в точке х₂.

В общем случае метод Рунге-Кутта применяется на произвольном разбиении отрезка [х₀, X]на п частей, т. е. с переменным шагом

x₀, x₁, ..., x_n; h_i = x_i_{+ 1}– x_i, x_n = X. (7.11)

Параметр α выбирают равным 1 или 0,5. Запишем окончательно расчетные формулы метода Рунге-Кутта второго порядка с переменным шагом для α = 1:

y_i₊ ₁ = y_i + h_i f(x_i + 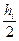, y_i + 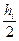f(x_i, y_i)), (7.12)

i = 0, 1, ..., n – 1.

и α = 0,5:

y_i₊ ₁ = y_i + 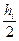[f(x_i, y_i)+ f(x_i + h_i, y_i + h_if(x_i, y_i))], (7.13)

i = 0, 1, ..., n – 1.

Дадим геометрическую интерпретацию методов Рунге-Кутта (7.12), (7.13).

На рис. 7.3 а иллюстрируется формула (7.12). Сначала по методу Эйлера вычисляется приближенное значение в точке х_i + h_i/2. В этой точке определяется касательная к интегральной кривой, параллельно которой через точку (x_i, y_i)проводится прямая до точки пересечения с прямой х = x_i ₊ ₁.Ордината точки пересечения y_i ₊ ₁ принимается за приближенное значение искомого решения в точке x_i ₊ ₁.

Рис. 7.3, б интерпретирует формулу (7.13). Методом Эйлера вычисляется приближенное значение y_i + h_if(х_i, y_i) в точке х_i ₊ ₁.В этой точке тангенс угла наклона касательной к интегральной кривой равен выражению f(x_i + h_i, y_i + h_if(х_i, y_i)).Через точку (x_i, у_i) проводится прямая, тангенс угла наклона которой определяется как полусумма угловых коэффициентов касательных, проведенных через точки (x_i, y_i) и (x_i ₊₁, y_i + h_if(x_i, у_i)).За приближенное значение искомого решения в точке х_i ₊₁ принимается ордината точки пересечения этой прямой с прямой х = x_i₊₁.

Отметим, что метод (7.13) совпадает с методом Эйлера-Коши (7.7).

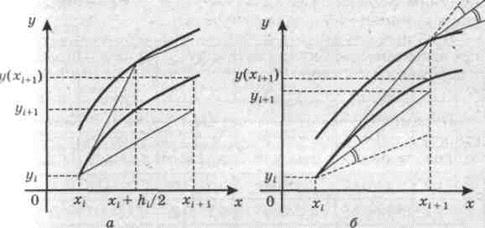
Рис. 7.3

Теорема 7.2. Если правая часть f(х, у)уравнения (7.1) непрерывна и ограничена вместе со своими производными до второго порядка включительно, то решение, полученное по формулам (7.12) и (7.13), равномерно сходится к решению задачи (7.1) и (7.2) с погрешностью O(max h_i²).

Приведем наиболее употребительные формулы метода Рунге-Кутта, формулы четвертого порядка точности:

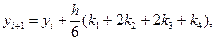
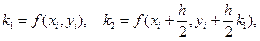(7.14)

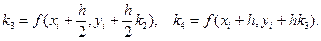
7.5. Метод Рунге-Кутта с автоматическим выбором шага. Правило Рунге оценки погрешности

Для метода Рунге-Кутта применимо правило Рунге для оценки погрешности. Пусть у(х; h) - приближенное значение решения в точке х, полученное по формулам (7.12), (7.13) или (7.14) с шагом h, а р - порядок точности соответствующей формулы. Тогда погрешность R(h) значения у(х; h) можно оценить, используя приближенное значение у(х; 2h) решения в точке х, полученное с шагом 2h:

R(h) = 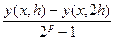(7.15)

где р = 2 для формул (7.12) и (7.13) и р = 4 для (7.14).

Уточненное решение запишем в виде

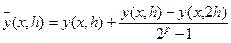(7.16)

В алгоритмах с автоматическим выбором шага предварительно задают погрешность в виде положительного параметра ε, и на каждом этапе вычисления следующего значения y_i ₊ ₁ подбирают такой шаг h, при котором выполняется неравенство

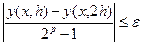(7.17)

7.6. Задача Коши для системы дифференциальных уравнений

Метод Рунге-Кутта применим и к задаче Коши для системы m дифференциальных уравнений первого порядкa с m неизвестными функциями

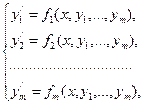x Î (x₀, X) (7.18)

y₁(x₀) = y_1,0, y₂(x₀) = y_2,0,…, y_m(x₀) = y_m_,0 (7.19)

Приведем для задачи (7.18), (7.19) расчетные формулы метода Рунге-Кутта четвертого порядка. Пусть требуется найти систему т функций у₁(х), у₂(х),..., у_m(х), удовлетворяющих в интервале (х₀, X) дифференциальным уравнениям (7.18), а в точке х₀ - начальным условиям (7.19). Предположим, что отрезок [х₀, X] разбит на N частей:

x_i = х₀ + ih, h = .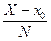

Тогда каждую l-ю функцию у_l(х) можно приближенно вычислять в точках х_i ₊₁ по формулам Рунге-Кутта

K_l_,1 = f_l(x_i, y_1,i, y_2,i,… ,y_m_,i), i = 1, 2, ... , m,

K_l_,2 = f_l(x_i + 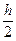, y_1,i + 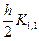, y_2,i+ 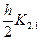,… ,y_m_,i + ),

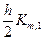i = 1, 2, ... , m;

K_l_,3 = f_l(x_i + 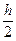, y_1,i + 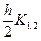, y_2,i+ 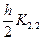,… ,y_m_,i + ),

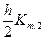i = 1, 2, ... , m;

K_l_,4 = f_l(x_i + h, y_1,i + 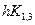, y_2,i+ 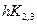,… ,y_m_,i + ),

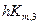i = 1, 2, ... , m;

y_l_,i+1 = y_l,i + 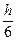( 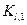+ + 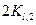+ 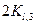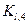), (7.20)

i = 1, 2, ... , m;

Здесь через у_l_,_i обозначено приближенное значение функции у_l(х) в точке х_i.

Необходимо обратить внимание на порядок вычислений по формулам (7.20). На каждом шаге сначала вычисляются коэффициенты K_l_,_i в следующем порядке:

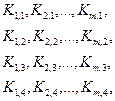
и лишь затем приближенные значения функций y_1,_i₊₁, y_2,_i₊₁,…, y_m_,_i₊₁.

7.7. Задачи Коши для дифференциальных уравнений высших порядков

Задача Коши для дифференциального уравнения n-го порядка

y⁽ⁿ⁾ = f(x, у, у', ... , y⁽ⁿ^-1)), x Î (х₀, X), (7.21)

y(x₀) = y₀, y'(x₀) = y_1,0,…,y⁽^п^-1)(x₀) = y_п _- _1,0. (7.22)

легко сводится к задаче Коши для системы дифференциальных уравнений первого порядка с помощью замены переменных

z₀ = y, z₁ = y',..., z_n _- ₁ = y⁽ⁿ^–¹⁾. (7.23)

Учитывая (7.23), из уравнения (7.21) получим систему дифференциальных уравнений

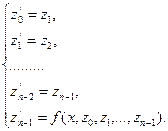(7.24)

Начальные условия (7.22) для функций z_l, переписываются в виде

z₀(x₀) = y₀, z₁(x₀) = y_1,0,…,z_n-₁(x₀) = y_п _- _1,0. (7.25)

Запишем для полученной системы метод Рунге-Кутта:

z_l_,_i₊₁ = z_l_,_i + 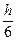( 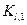+ + 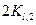+ 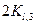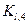), (7.26)

i = 0, 1, 2, ... , N; l = 0, 1,…, n – 1.

Для вычисления коэффициентов 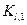, , 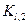, 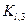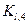имеем следующие формулы:

K_0,1 = z_1,i,

K_1,1 = z_2,i,

…………

K_n_-1,1 = f(x_i, z_0,i, z_1,i,…, z_n_-1,i),

K_0,2 = z_1,i + ,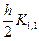

K_1,2 = z_2,i + ,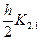

…………………

K_n_-1,2 = f(x_i + 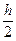, z_0,i + 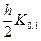, z_1,i+ 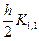,…, z_n_-1,i + ),

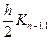K_0,3 = z_1,i + ,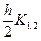

K_1,3 = z_2,i + ,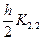

…………………

K_n_-1,3 = f(x_i + 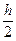, z_0,i + 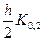, z_1,i+ 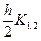,…, z_n_-1,i + ),

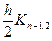K_0,4 = z_1,i + ,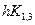

K_1,4 = z_2,i + ,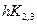

K_n_-1,4 = f(x_i + 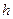, z_0,i + 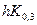, z_1,i+ 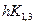,…, z_n_-1,i + ).

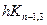7.8. Краевые задачи для обыкновенных дифференциальных уравнений

Примерами краевых задач для обыкновенных дифференциальных уравнений являются следующие:

1) Найти функцию u(х), которая удовлетворяет на отрезке [а, b] уравнению

u"(х) = -f(х), (7.27)

а на концах отрезка условиям

u(а) = u (b) = 0. (7.28)

Задача (7.27), (7.28) имеет следующее физическое содержание. Между точками х = а и х = b натянута упругая струна, находящаяся под действием внешней изгибающей нагрузки. f(x) - величина нагрузки, а u(х) - прогиб струны в безразмерных единицах.

2) Двухточечная краевая задача для линейного дифференциального уравнения второго порядка:

u"(x) + p(x)u'(x) + q(x)u(x) = f(x), (7.29)

α₀u(a) + α₁u'(a) = A,

β₀u(b) + β₁u'(b) = B. (7.30)

а) Метод прогонки

Рассмотрим частный случай задачи (7.29), (7.30):

u"(x) + p(x)u'(x) + q(x)u(x) = f(x), (7.31)

u(0) = а, u(Х) = b. (7.32)

Введем сетку x_i = ih, i = 1, 2, ... , N; h = X/N. Обозначим через u_i приближенные значения u(x) в узлах сетки. Рассмотрим уравнение (7.31) во внутренних узлах х_i i = 1, 2,..., N - 1и заменим производную второго порядка разностной формулой (5.11)

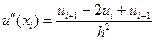(7.33)

Тогда из (7.31), (7.32) получим для определения u_i систему линейных уравнений

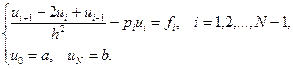(7.34)

Система (7.34) при р(x) ≥ 0 имеет решение. Система (7.34) представляет собой систему линейных уравнений с трехдиагональной матрицей

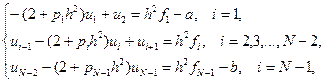(7.35)

и для ее решения применим метод прогонки, который фактически является методом исключения неизвестных Гаусса.

1. Прямой ход прогонки. Запишем первое уравнение (7.35) в виде

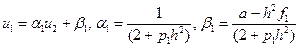. (7.36)

Подставив (7.36) во второе уравнение (7.35) и упростив выражения, увидим, что можно для u_i получить формулы

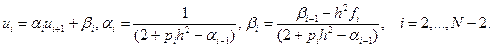(7.37)

Из уравнения (7.35), учитывая (7.37) при i = N - 2, получим

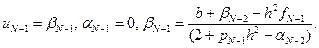(7.38)

2. Обратный ход прогонки. После вычисления прогоночных коэффициентов можно найти значения решения задачи. Формула (7.38) дает значение

u_N _- ₁:

u_N _- ₁ = β_N _{- 1}(7.39)

Остальные значения вычисляем в обратном порядке:

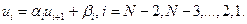(7.40)

б) Метод стрельбы (пристрелки)

Рассмотрим метод пристрелки на примере решения линейной краевой задачи (7.31), (7.32):

u"(x) + p(x)u'(x) + q(x)u(x) = f(x),

u(0) = а, u(Х) = b.

Если известны частное решение u(х) неоднородного уравнения

u"(x) + p(x)u'(x) + q(x)u(x) = f(x),

и два линейно независимых решения и₁(х), u₂(х) однородного уравнения

u"(x) + p(x)u'(x) + q(x)u(x) = 0,

то общее решение неоднородного дифференциального уравнения

u"(x) + p(x)u'(x) + q(x)u(x) = f(x),

можно записать в виде

u(x) + С₁u₁(х) + C₂u₂(x).

Постоянные С₁, С₂ можно определить из краевых условий (7.32).

В методе пристрелки используется следующий способ.

Сначала находят частное решение u(х) неоднородного уравнения

u"(x) + p(x)u'(x) + q(x)u(x) = f(x),

удовлетворяющее условию u(0) = а, и частное решение u₁(х) однородного уравнения

u"(x) + p(x)u'(x) + q(x)u(x) = 0,

удовлетворяющее условию u(0) = 0.

Затем общее решение u(х) неоднородного уравнения

u"(x) + p(x)u'(x) + q(x)u(x) = f(x),

удовлетворяющее условию u(0) = а, записывают в виде u(х) + Сu₁(х). Остается найти постоянную С₁ из условия u(x) + Cu₁(x) = b.

Приведем сеточный аналог метода пристрелки. Пусть краевая задача приведена к системе уравнений (7.34)

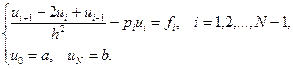(7.41)

Найдем частные решения неоднородной (7.42) и однородной (7.43) систем уравнений:

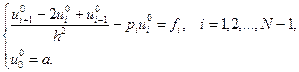(7.42)

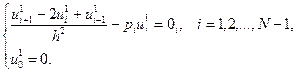(7.43)

Выбирая произвольные значения для 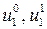(при этом должно быть 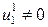), находим из (7.42) и (7.43) формулы для вычисления частных решений:

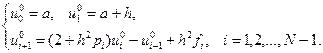(7.44)

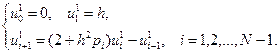(7.45)

Найдем С из условия 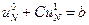и запишем решение:

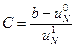(7.46)

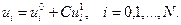(7.47)

Алгоритм метода пристрелки заключается в том, чтобы выбрать шаг h и выполнить последовательно вычисления по формулам (7.44) - (7.47).

<== предыдущая лекция | следующая лекция ==>

Численное интегрирование | Уравнения в частных производных

Дата добавления: 2020-08-31; просмотров: 383;

Поиск по сайту

Узнать еще

Публикации по технике и механике

Публикации по биологии

Публикации по информатике

Публикации по строительству

Публикации по физике

Публикации по химии

Публикации по электронике

Публикации по искусству

Публикации по истории

Публикации по медицине

Разделы публикаций

<== предыдущая лекция	\|	следующая лекция ==>
Численное интегрирование	\|	Уравнения в частных производных