Розділ 5. Основи теорії коливань мембрани

В попередніх матеріалах були розглянуті коливання систем з зосередженими параметрами і найпростіші одновимірні моделі систем з розподіленими параметрами – модель струни і стрижня (поздовжні коливання). Перед вивченням акустичних процесів в різних середовищах доцільно розглянути приклади двовимірних коливальних рухів.

рис. 1.1

Побудуємо математичну модель мембрани. Мембрана – ідеально гнучка, нескінченно тонка плоска поверхня, яка має дві властивості: масу, яка задається масою одиниці поверхні мембрани 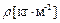і відновлюючу силу, яка прагне повернути елемент поверхні у стан рівноваги. Така сила створюється за рахунок попереднього всебічного натягу мембрани, що характеризується величиною 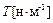- силою, яка діє на одиницю довжини елемента мембрани. Така абстрактна модель мембрани досить близька за властивостями до мембрани барабана чи барабанної перетинки вуха.

рис. 1.2

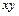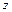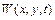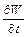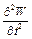Виведемо диференціальні рівняння руху елемента мембрани. Для цього розглянемо нескінченно малий елемент поверхні мембрани. Дію відкинутої частини слід замінити пружними силами, що розподілені вздовж контуру виділеного елемента мембрани. Сумістимо площину з поверхнею недеформованої мембрани. Відхилення точок мембрани від положення рівноваги в напрямі осі опишемо величиною . Частинні похідні і відповідають коливальній швидкості і прискоренню елемента мембрани.

Запишемо проекцію на вісь 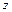співвідношення другого закону Ньютона для елемента мембрани зі сторонами 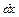і .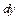

Крім указаних сил, пов’язаних з наявністю натягу (пружні сили) та сил інерції, на мембрану може впливати додаткова зовнішня сила, яку можна охарактеризувати поверхневою густиною 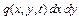, що напрямлена вздовж осі .

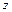У відповідності з рис.1.2 знайдемо проекцію на вісь 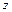пружних сил, що діють по сторонах 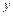та 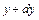виділеного елемента

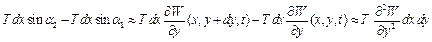
(1.1.а)

Аналогічно отримаємо проекцію пружних сил, що діють по сторонах 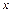та 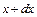виділеного елемента на вісь .

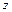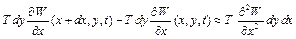(1.1.б)

З урахуванням того, що маса виділеного елемента дорівнює 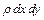, а зовнішні сили - 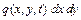, одержимо наступне диференціальне рівняння елемента мембрани

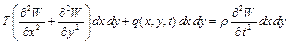(1.2.а)

або

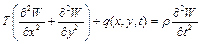(1.2.б)

В математичній фізиці існує спеціальне позначення 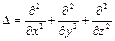в декартових координатах. Цей вираз носить назву оператора Лапласа. Тоді диференціальне рівняння руху елемента мембрани має вид

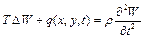, (1.3)

де .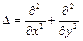

Якщо зовнішні сили на мембрану не діють 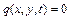, то рівняння (1.3) набуває вигляду

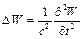, (1.4)

де 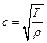- фазова швидкість пружних хвиль в мембрані.

Рівняння (1.4) носить назву хвильового рівняння для випадку двох просторових координат.

В мембрані можливі хвильові рухи такого характеру, як і для системи паралельних струн. Наприклад, вираз

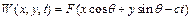(1.5)

задовольняє хвильове рівняння. Такий вираз являє собою хвилю, яка поширюється зі швидкістю 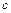у напрямі, що складає кут 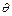з віссю 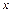. Хвильові фронти, що являють собою лінії постійної фази, 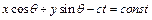, перпендикулярні цьому напряму. Такі хвилі називаються лінійними хвилями. Оскільки хвильове рівняння – лінійне, то сума будь-якого числа його розв’язків також є розв’язком. При цьому певні комбінації хвильових рухів типу (1.5) можуть спричинити набагато складніші хвилі. Так, виходячи з останнього розв’язку (1.5), можна побудувати вираз

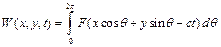(1.6)

який також задовольняє хвильове рівняння. Проте такий розв’язок вже не є лінійною хвилею.