Пружні хвилі у складному стрижні

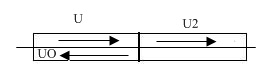
У багатьох практичних випадках вивчення коливальних процесів у одній механічній системі, можна дістати лише з урахуванням її взаємодії з іншими системами. В цьому разі граничні умови повинні бути замінені на умови спряженості між коливальними системами. У загальному випадку такі умови відображають фізичні властивості обох взаємодіючих систем. Характер таких умов і способи їх описання розглянемо на найпростішому прикладі напівнескінченних стрижнів з різних матеріалів (рис 4.30)

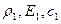0

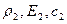
Припустимо, що в лівому стрижні ( 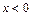) з нескінченності до перерізу поширюється хвиля

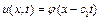
При падінні хвилі на межу розподілу матеріалів 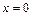частина хвильової (коливальної) енергії відбивається, а частина пройде у другий стрижень. Необхідно знайти відбиту хвилю і хвилю, що пройшла.

Розглянемо умови спряженості двох стрижнів на поверхні 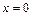. Ці умови для будь-яких систем містить у собі кінематичні та силові співвідношення.

В даному випадку складеного стрижня кінематична умова полягає в тому, що в процесі відбиття хвилі на поверхні контакту ( 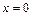) не можуть виникнути розриви хвилі, тобто.

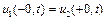(4.94)

де, 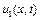являє собою суму кожної суму падаючої та відбитої хвилі( 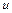) та відбитої хвиль ( 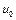) хвиль (рис. 4.30) в лівій частині стрижня.

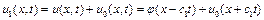
а 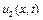- хвиля, що розповсюджується в правій частині стрижня.

Оскільки швидкість поширення збурень у правій частині стрижня дорівнює 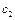, зміщення точок стрижня від положення рівноваги 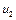є функцією фази хвилі аргументу, що пройшла .

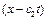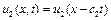
Друга, силова, умова спряженості складного стрижня відображає вимогу третього закону про рівність дії і протидії на поверхні контакту ( ):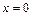

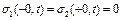(4.95)

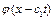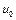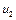Для того щоб співвідношення виконувалися в будь-який момент часу при заданій функції , функції і при 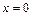мають бути пропорційними 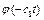. Ця вимога виконується, якщо показати:

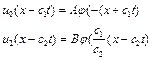(4.96)

Тут A і B - довільні сталі, що характеризують ступінь збудження відбитої хвилі, та хвилі, яка пройшла.

Перша умова спряженості (4.94) з урахуванням (4.96), приводить до наступного алгебраїчного рівняння для системи A і B:

1+A=B (4.97)

Для виконання другої умови спряження (4.95) слід скористатися законом Гука ( )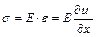

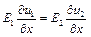( при )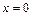

При цьому для деформації ( 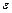) матимемо такі вирази:

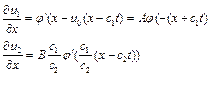
Штрих у знака функції вказує на похідну по її головному аргументу.

Тоді силова умова спряженості (при 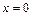), зводиться до такої алгебраїчної рівності.

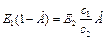(4.98)

Якщо врахувати визначення швидкості хвиль 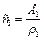, , 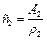то з системи рівнянь (4.96) і (4.97) отримаємо наступні значення довільних сталих A і B:

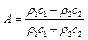(4.99)

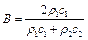(4.100)

Співвідношення ( 4.99) між відбитою хвилею (А) та хвилею, що пройшла, повністью визначаються відношенням хвильових опорів( ).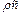

Причому , якщо 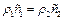, тобто права частина стрижня ( 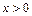) може відрізнятися від лівої як густиною так і швидкістю звуку, але хвильові опори частин стрижня однакові, то відбита хвиля відсутня(А=0). Це означає, що хвиля не помічає різниці у властивостях матеріалів, коли їх хвильові опори збігаються.

Аналіз виразу (4.98) для коефіцієнта відбиття А дозволяє виділити два крайніх випадки, що відповідають розглянутим граничним умовам (4.94) і (4.95). Якщо хвильові опори такі що 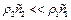, матимемо 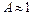. Хвиля що падає повністю відбивається при цьому напруги на межі прагнуть до нуля(вільний кінець). Якщ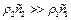о то 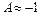. У цьому разі хвиля, що падає, також повністю відбивається, проте зміщення на межі поділу стає рівним нулю(жорстко защемлений кінець).

Проведення аналізу примушує звернути увагу на деяку незвичайність розглянутих граничних випадків. Якщ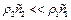о , то 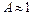. Проте тоді 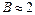, тобто зміщення (4.100) хвилі, що пройшла, у два рази перевищує зміщення у хвилі, що падає. Ця обставина примушує більш чітко визначатися зі змістом висловлювання падаюча хвиля повністю відбивається. Це тим більш важливо, оскільки має парадокс і другий розглянутий граничний випадок , 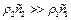. Якщо при цьому при прийняти, що 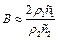, то із співвідношення ( 4.95), що відображає умови рівності напруг на поверхні контакту стрижнів ( 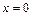), знаходимо:

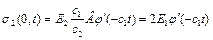
Тобто напруги у хвилі, що пройшла, у два рази перевищують напруги в падаючій хвилі.

У цілому одержаний результат дозволяє сформулювати загальний висновок при переході хвилі із більш жорсткого середовища у більш м’яке ( 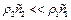) зростають зміщення( а, відповідно і швидкості) частинок середовища.

При переході хвилі з м’якого середовища у більш жорстке( 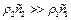) напруги у хвилі, що пройшла, зростають. Встановленню, що гранична величина коефіцієнтів. Збільшення вказаних характеристик хвиль дорівнює двом.