Вимушені коливання струни з урахуванням демпфірування

Розглянемо струну довжиною l, що закріплена на кінцях. Нехай функція 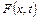характеризує зовнішню силу на одиницю довжини струни. Припустимо, що 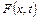не залежить від руху струни, тобто являє собою джерело сили нескінченної пружності.

Для багатьох коливальних систем в акустиці, крім процесу перетворення механічної енергії в теплоту при деформації елемента струни, суттєвим механізмом розсіювання енергії є витрати на випромінювання, тобто втрати енергії за рахунок звукових хвиль, що біжать від тіла, що здійснює коливання. У багатьох практично важливих акустичних системах такі втрати на випромінювання суттєво перевищують втрати енергії у матеріалі. У випадку тонкої струни втрати на випромінювання дуже малі. Більш суттєвими втратами в реальній струні є втрати в опорах, тобто втрати, пов’язані з переходом енергії від коливаючої струни до того об’єкту, на якому закріплена струна. У музичних інструментах саме за рахунок таких втрат створюється звук у навколишньому середовищі.

Розглянемо найпростіший механізм впливу демпфірування на коливання струни.

Як і у випадку систем з зосередженими параметрами припускаємо, що сила опору на одиницю довжини струни пропорційна швидкості руху елемента струни з коефіцієнтом пропорційності R. Для елемента струни довжиною dx проекція сили опору на вісь y дорівнюватиме .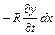

Таким чином, рівняння руху елементу струни набирає вигляду:

,

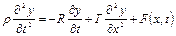або:

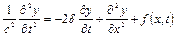, (4.69)

де , , .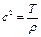

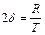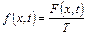Нехай зовнішня сила – періодична за часом:

.

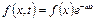Розв’язок рівняння (4.69) складається з власних та вимушених коливань. Розглянемо усталені коливання струни, тобто її рухи в ті моменти часу, коли вільні коливання вже згасли. Частковий розв’язок рівняння

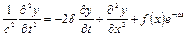(4.70)

будемо шукати у вигляді:

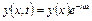. (4.71)

Підставляючи (4.71) в (4.70), отримаємо:

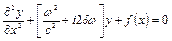. (4.72)

Частковий розв’язок цього рівняння має задовольняти граничним умовам на кінцях струни. Тому, при побудові розв’язку доцільно використовувати властивості нормальних форм коливань ідеальної струни 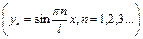. Представимо в вигляді рядів Фур’є по власним (нормальним) формам коливань струни зовнішнє збурення 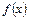та шуканий частинний розв’язок :

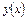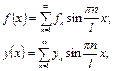(4.73)

де 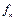– відомі коефіцієнти при заданому розподілі зовнішньої сили в ряд Фур’є:

,

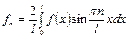а величини 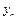підлягають визначенню. Після підстановки (4.73) у (4.72) дістанемо:

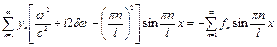, (4.74)

тоді:

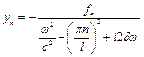. (4.75)

Останнє співвідношення визначає значення величин 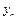через задані коефіцієнти 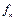розкладання зовнішньої сили в ряд Фур’є.

Остаточно вимушені коливання елемента струни описуються наступним виразом:

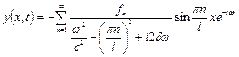, (4.76)

або:

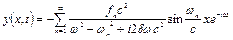, (4.77)

де 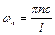– частота власних (нормальних) коливань струни.

Ряд (4.77) розкриває явище резонансу.

Покладемо 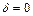, тобто при коливаннях струни демпфірування не враховується. Тоді для виникнення резонансу необхідно виконання двох умов: перше – наближення частоти зовнішньої сили 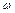до однієї з власних частот струни 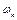; друга – наявність у просторовому розподілі зовнішньої сили складової, що відповідає n-ій формі коливань. Якщо, наприклад, 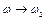, то необхідно виконання умови 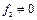. У противному разі резонанс не відбудеться. Якщо ці дві умови виконуються, то амплітуда руху з плином часу необмежено зростає і форма струни наближається до форми, що відповідає даній моді коливань.

Залежність вимушеного руху струни від характеру зовнішнього навантаження часто виявляється при збудженні її зосередженою силою. Якщо сила прикладається у вузлі однієї з нормальних мод, то така мода в русі відсутня. Це широко використовується при проектування музичних інструментів. Відомо, що характер звучання має неприємний відтінок, коли разом з основним тоном збуджуються гармоніки високих частот (починаючи з 8-ої). Тому в роялі місце удару молоточка вибирають близько від точки закріплення струни між вузлами 8-ої та 9-ої гармонік, щоб зменшити їх енергію збудження. Регулюючи ширину молоточка, та його жорсткість, прагнуть збільшити відносну енергію низьких гармонік (4-ої і 5-ої). Для такого удару частина молоточка виготовляється із спеціального підібраного матеріалу.

Повернемося до виразу (4.76). Тут добре видно, що ступінь збудження кожної власної форми коливань залежить від ступеня близькості заданого хвильового числа 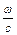і хвильового числа власної форми 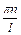. У разі резонансу, тобто 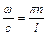, де n – деякий фіксований номер, амплітуда коливань струни залишається скінченною. Вплив демпфірування при вимушених коливаннях струни відображується на тих формах, для яких можна вважати:

.

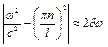Для тих власних форм, де 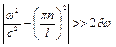наявність демпфірування несуттєва. Слід також звернути увагу на аналогію знаменника (4.76) з комплексним механічним імпедансом Z системи з одним ступенем вільності. У випадку системі з розподіленими параметрами можна говорити про комплексний імпеданс кожного нормального коливання.