Поздовжні хвилі у пружному стрижні (поздовжні коливання пружного стрижня)
Крім струни, ще однією одновимірною системою з розподіленими параметрами є стрижень.
Стрижень – фізичне тіло довгастої форми, в якому поперечний розмір набагато менший за довжину (D<<L, якщо, наприклад, стрижень циліндричної форми).
На відміну від струни стрижень має значну поперечну жорсткість. Розрізняють три типи коливань стрижня:
· повздовжні;
· крутильні;
· поперечні.
Розглянемо більш детально поздовжні коливання.
 Будемо вважати, що всі поперечні перерізи стрижня x=const (рис.4.27) у процесі деформації залишаються плоскими і зміщуються паралельно один одному.
Будемо вважати, що всі поперечні перерізи стрижня x=const (рис.4.27) у процесі деформації залишаються плоскими і зміщуються паралельно один одному.
| рис.4.27 |
Відновлюючи сила в струні забезпечувалась за рахунок попереднього натягу. У випадку пружного стрижня така сила визначається внутрішніми пружними силами, що виникають при зміні відстані між частинками пружного тіла. В механіці деформованого твердого тіла ці сили характеризуються напругою σ, тобто величиною сили на одиницю площі. При коливаннях пружного стрижня припускаємо, що внутрішні напруги в кожному перерізі стрижня σ(х) рівномірно розподілені по його перерізу. Якщо відносне видовження стрижня  , де
, де  - початкова довжина, а
- початкова довжина, а 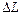 - видовження стрижня, то модуль пружності знаходиться з виразу
- видовження стрижня, то модуль пружності знаходиться з виразу
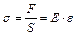 , (4.78)
, (4.78)
причому 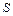 - площа поперечного перерізу стрижня,
- площа поперечного перерізу стрижня, 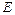 - модуль Юнга.
- модуль Юнга.
Співвідношення (4.78) являє собою закон Гука, виражений через напругу та видовження за умови малих деформацій 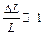 .
.
Рух точок стрижня у рамках прийнятих припущень можна описати функцією u(x,t), що характеризує зміщення точок стрижня відносно положення рівноваги.
У відповідності з принципом Д'Аламбера сили, що діють на елементарний відрізок стрижня довжиною dx (рис.4.28) будуть дорівнювати

|
| рис.4.28 |
 , (4.79)
, (4.79)
де 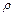 - густина матеріалу стрижня, а
- густина матеріалу стрижня, а  - елементарна маса одиничного елементу стрижня. Рівняння (4.79) можна привести до вигляду
- елементарна маса одиничного елементу стрижня. Рівняння (4.79) можна привести до вигляду
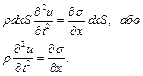 (4.80)
(4.80)
Підставивши вираз (4.78) у формі 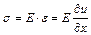 в рівняння (4.80) отримаємо диференціальне рівняння руху елемента стрижня
в рівняння (4.80) отримаємо диференціальне рівняння руху елемента стрижня
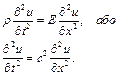 (4.81)
(4.81)
де 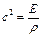 - деяка константа, що характеризує швидкість розповсюдження поздовжніх хвиль у стрижні.
- деяка константа, що характеризує швидкість розповсюдження поздовжніх хвиль у стрижні.
Рівняння поздовжнього руху елемента стрижня за формою повністю збігається з рівнянням, що описує поперечні коливання елемента струни. Це дозволяє стверджувати, що його розв'язок співпадає з розв'язком, отриманим для диференціального рівняння вільних коливань струни.
Покажемо, крім того, що розв'язком рівняння (4.81) може бути сума двох функцій зі спеціальними аргументами:
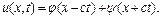 (4.82)
(4.82)
Неважко переконатися, що вираз
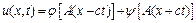 , (4.83)
, (4.83)
де А – деяка стала, також є розв'язком рівняння (4.81).
З'ясуємо фізичний зміст функцій (4.82). Розглянемо одну зі складових цієї функції, наприклад, 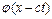 .
.
В деякій фіксованій точці х=х1 у момент часу t=t1 ця складова має вид 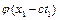 . Через деякий час
. Через деякий час 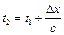 , де
, де 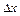 - відстань від точки х1 до точки
- відстань від точки х1 до точки 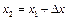 ця складова
ця складова
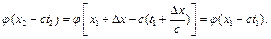
Тобто, збурений стан в стрижні, який спостерігається в точці х1 в момент t1, зберігається таким самим у точці 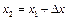 з плином часу
з плином часу 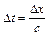 (рис.4.29).
(рис.4.29).

|
| рис.4.29 |
Отже, функція 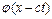 описує перенесення збурення вздовж стрижня у напрямку зростання х зі швидкістю с. Аналогічно, функція
описує перенесення збурення вздовж стрижня у напрямку зростання х зі швидкістю с. Аналогічно, функція 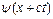 описує перенесення збурення в напрямку зменшення х з тією самою швидкістю с.
описує перенесення збурення в напрямку зменшення х з тією самою швидкістю с.
Фізичне явище, що описується такою математичною залежністю називається рухомою хвилею. При цьому аргументи функцій 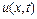 -
- 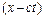 і
і 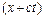 називають фазою хвилі, а сталу величину с – фазовою швидкістю.
називають фазою хвилі, а сталу величину с – фазовою швидкістю.
Отже, функція (4.83) являє собою суму хвиль, що біжать у протилежних напрямках. На відміну від струни, де швидкість руху частинок струни напрямлена перпендикулярно до рівноважного положення, тут напрям поширення хвиль і рух елементарних частинок стрижня збігаються. Такі хвильові рухи називаються поздовжніми хвилями, на відміну від поперечних хвиль в струні, коли швидкість руху частинок струни напрямлена перпендикулярно до положення рівноваги, а хвильове збурення поширюється вздовж струни.
Визначимо хвильовий (комплексний) опір стрижня для поздовжніх хвиль у ньому.
Під хвильовим опором розуміють відношення внутрішньої сили в деякому перерізі до швидкості руху точки прикладання сили, тобто
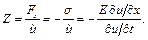 (4.84)
(4.84)
Для хвилі 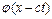
 (4.85)
(4.85)
де 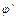 - похідна по повному аргументу, а для хвилі
- похідна по повному аргументу, а для хвилі 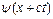
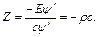 (4.86)
(4.86)
В загальному випадку значення хвильового опору несе інформацію і про напрям поширення хвилі. Така сама картина має місце для хвильового опору в струні.
Зауважимо, що добуток густини середовища на фазову швидкість хвилі характеризує хвильовий опір найрізноманітніших середовищ.
Розглянемо типові граничні умови для стрижня:
а) кінець стрижня (х=1) защемлений, що означає відсутність зміщення на кінці стрижня в певний момент часу, тобто
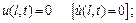 (4.87)
(4.87)
б) кінець стрижня (х=1) вільний, що означає відсутність напруг на кінці стрижня в певний момент часу, тобто
 . (4.88)
. (4.88)
Визначимо нормальні коливання стрижня довжини 1 за різними граничними умовами.
1. Кінці стрижня вільні:
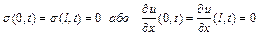 .
.
Шукаємо розв'язок рівняння (4.72) у вигляді
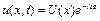 . (4.89)
. (4.89)
Підставляючи (4.89) в (4.81), отримаємо
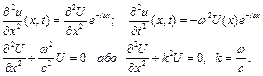 (4.90)
(4.90)
Розв'язок рівняння (4.90) має вид
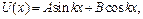 а (4.91)
а (4.91)
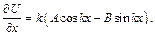 (4.92)
(4.92)
З умови 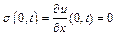 маємо А=0.
маємо А=0.
З умови 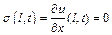 отримаємо
отримаємо
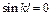 або
або  , або
, або 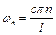 . (4.93)
. (4.93)
Отже, при вільних кінцях стрижня нормальні частоти знаходяться з виразу 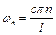 і створюють гармонічний ряд, а форми коливань визначаються через
і створюють гармонічний ряд, а форми коливань визначаються через 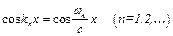 .
.
2. Один кінець стрижня вільний, інший – защемлений:
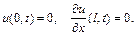
Із загального розв'язку (4.82), з урахуванням граничних умов
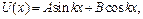
знаходимо, що В=0, coskl=0, звідки
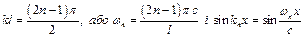
3. Обидва кінці стрижня защимлені:
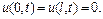
Виконавши відповідні операції отримаємо
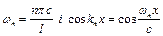 ,
,
тобто нормальні частоти в першому і третьому випадках збігаються.
Дата добавления: 2020-08-31; просмотров: 756;











