Вільні коливання круглої мембрани
Для вивчення коливань круглої мембрани, защемленої по зовнішньому контуру, використовують полярні координати 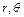 . У цьому разі шукана функція
. У цьому разі шукана функція 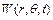 визначається з хвильового рівняння
визначається з хвильового рівняння
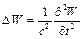 ,
,
де 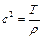 , а оператор Лапласа має вид
, а оператор Лапласа має вид
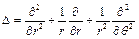 (3.1)
(3.1)
Тоді хвильове рівняння має вид:
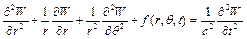 , (3.2)
, (3.2)
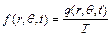 .
.
У разі вільних коливань мембрани радіуса 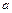 зовнішнє розподілення навантаження відсутнє
зовнішнє розподілення навантаження відсутнє 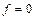 і функція
і функція 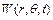 , яка знаходиться з однорідного рівняння, має задовольняти граничні
, яка знаходиться з однорідного рівняння, має задовольняти граничні
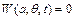 (3.3)
(3.3)
та початкові умови
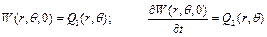 . (3.4)
. (3.4)
Функцію відхилення точок мембрани від положення рівноваги шукаємо у вигляді
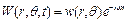 . (3.5)
. (3.5)
Робимо припущення про існування розв’язку 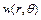 для круглої мембрани, як добутку двох незалежних функцій
для круглої мембрани, як добутку двох незалежних функцій
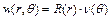 .
.
Після підстановки у хвильове рівняння маємо
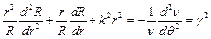 (3.6)
(3.6)
З останнього рівняння отримаємо 2 незалежних рівняння:
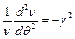 або
або 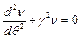 (3.7)
(3.7)
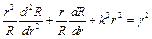 або
або 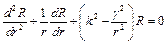 (3.8)
(3.8)
Розв’язок першого рівняння має вид
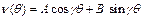 .
.
Оскільки розглядається кругла мембрана 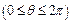 , то і розв’язок
, то і розв’язок 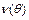 має бути періодичною функцією кута
має бути періодичною функцією кута 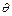 з періодом
з періодом 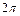 . Це можливо, коли стала
. Це можливо, коли стала 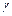 дорівнює цілому числу, тобто
дорівнює цілому числу, тобто 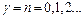
Після цього друге рівняння (3.8) набирає вигляду
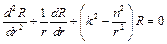 (3.9)
(3.9)
Останнє рівняння, що виникає у багатьох різних задачах фізики дістало назву рівняння Бесселя, який дослідив його властивості. Останнє рівняння є рівнянням другого порядку і повинно мати два лінійно незалежних розв’язки, для яких прийнято спеціальні позначення 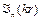 ,
, 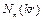 . Перше з них називається функцією Бесселя першого роду, а друге – функцією Бесселя другого роду (інакше функцією Неймана) n-го порядку (див рис. 3.1).
. Перше з них називається функцією Бесселя першого роду, а друге – функцією Бесселя другого роду (інакше функцією Неймана) n-го порядку (див рис. 3.1).
Про характер функцій, що є розв’язками останнього рівняння можна судити порівнюючи зображення у вигляді ряду по степеням аргументу функції Бесселя першого роду 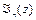 і звичайної функції, як
і звичайної функції, як 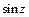 :
:
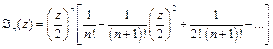 ; (3.10)
; (3.10)
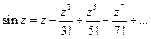 (3.11)
(3.11)
Аналіз функцій показує, що функції Бесселя досить близькі за своєю природою до відомих тригонометричних функцій.
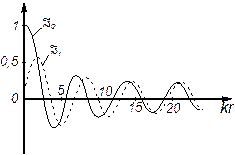
|
| а |
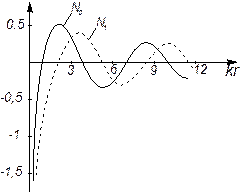
|
| б |
| рис. 3.1 |
Характерно, що всі функції другого роду при наближенні 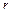 до нуля прямують у мінус нескінченність. Наприклад
до нуля прямують у мінус нескінченність. Наприклад
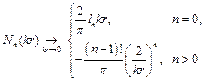 (3.12)
(3.12)
Враховуючи, що 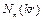 необмежено зростає при наближенні до центра мембрани, амплітуди прогину мембрани представляють у вигляді
необмежено зростає при наближенні до центра мембрани, амплітуди прогину мембрани представляють у вигляді
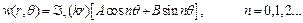 (3.13)
(3.13)
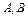 – деякі сталі.
– деякі сталі.
Існують осесиметричні (відносно напряму 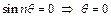 ) і неосесиметричні (
) і неосесиметричні ( 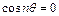 ) коливання мембрани. Розглянемо осесиметричні коливання. Тоді
) коливання мембрани. Розглянемо осесиметричні коливання. Тоді
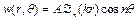 , (3.14)
, (3.14)
де 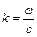 поки невідома довільна величина.
поки невідома довільна величина.
У відповідності з граничними умовами
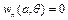 , а
, а 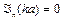 (3.15)
(3.15)
Якщо обмежитись асимптотичним виразом для функції Бесселя
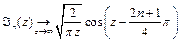 , (3.16)
, (3.16)
одержимо
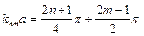 (3.17)
(3.17)
Нескінченний набір коренів (3.15) визначає нескінченний набір власних частот і форм коливань
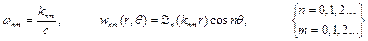 (3.18)
(3.18)
Форми коливань визначаються з точністю до сталого множника. В останньому виразі для форм коливань круглої мембрани обмежились лише 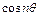 при запису кутової залежності (осесиметричні коливання). В загальному вигляді вираз для
при запису кутової залежності (осесиметричні коливання). В загальному вигляді вираз для 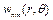 задовольнятиме рівняння Гельмгольца в полярних координатах, якщо замінити
задовольнятиме рівняння Гельмгольца в полярних координатах, якщо замінити 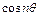 на
на 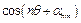 .
.
Як і у випадку прямокутної мембрани, кожна власна форма коливань мембрани є певна сукупність стоячих хвиль, що характеризуються своїми вузловими точками (лініями). У даному разі такими лініями є вузлові кола та вузлові діаметри, що визначаються відповідно рівняннями
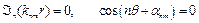 . (3.19)
. (3.19)
Перше з цих рівнянь визначає 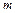 кіл, концентричних з контуром мембрани. Радіуси цих кіл
кіл, концентричних з контуром мембрани. Радіуси цих кіл
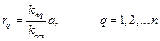 (3.20)
(3.20)
Радіус 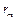 збігається з радіусом мембрани. Друге рівняння з (3.19) визначає
збігається з радіусом мембрани. Друге рівняння з (3.19) визначає 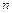 вузлових діаметрів мембрани
вузлових діаметрів мембрани
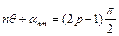 ,
,
або
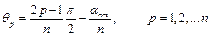 .
.
На рис 3.2 зображено деякі випадки розміщення вузлових ліній.

|
| рис. 3.2 |
Зазначимо, що співвідношення нормальних частот мембрани не є ціле число, тобто вони не створюють гармонічний ряд. Тому мембрана через період основного тону у попередній стан не повертається. Звичайно можна створити такі початкові умови, коли в коливаннях мембрани буде лише одне гармонічне коливання.
Дата добавления: 2020-08-31; просмотров: 827;











