Вільні коливання прямокутної мембрани

рис. 2.1

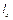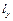Прямокутна мембрана зі сторонами та (рис. 2.1) закріплена по краям. У момент часу 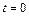задані початкові умови:

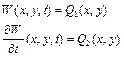(2.1)

Необхідно знайти функцію 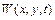, що задовольняє хвильове рівняння (1.4) з граничними умовами

;

.

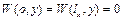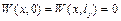Розв’язок рівняння будемо шукати у вигляді

.

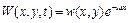Тоді

; ;

,

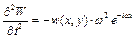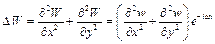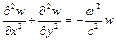або

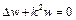, (2.2)

де .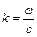

Описане рівняння носить назву рівняння Гельмгольца. Будемо шукати його розв’язок у вигляді добутку двох функцій, кожна х яких залежить від однієї координати

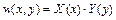. (2.3)

Тоді

; ,

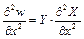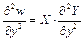(при чому 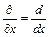для даного випадку).

З урахуванням останніх виразів рівняння Гельмгольца має вигляд

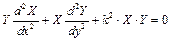(2.4.а)

або

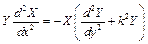. (2.4.б)

Розділимо обидві частини рівності на 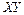, тоді отримаємо

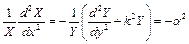, (2.5)

де 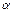– деяка стала величина

Аналізуючи (2.5), можна зробити висновок, що розв’язок рівняння Гельмгольца у вигляді добутку двох функцій, кожна з яких залежить від однієї змінної, існує, причому ці функції однозначно визначаються із наступних диференціальних рівнянь:

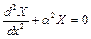(2.6)

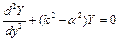(2.7)

Їхні загальні розв’язки мають вигляд

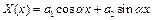(2.8)

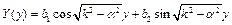(2.9)

де 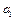, , 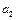, 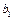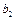– довільні величини .

Враховуючи граничні умови

(2.10)

отримаємо

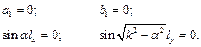(2.11)

Тоді

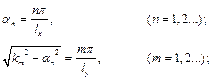(2.12.а)

або

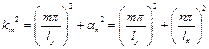(2.12.б)

Враховуючи, що ,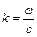

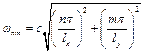(2.13)

Таким чином, коливання прямокутної мембрани можуть бути описані функцією

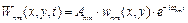; (2.14.а)

або в дійсній формі

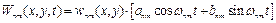, (2.14.б)

де 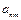, , –довільні дійсні числа.

Власні форми та власні частоти визначаються так:

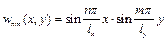, (2.15)

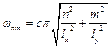. (2.16)

Проаналізуємо отримані результати. Розглянемо найпростіше коливання, що відповідає випадку 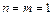( 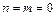фізичного змісту не має):

,

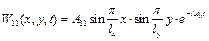де 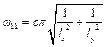– найменша нормальна частота, яка характеризує основний тон мембрани. Найбільшу амплітуду коливань матиме точка з координатами 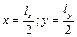, тобто центр мембрани. Як і для струни, такі точки називаються точками спучування. Лінії, точки яких не коливаються, називаються вузловими лініями. Для нормального коливання 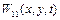вузлові лінії збігаються з контуром мембрани (рис. 2.2а).

Розглянемо нормальні коливання 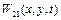. Вузлові лінії визначаються з рівнянь 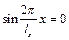і 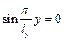. Крім точок на контурі мембрани, це буде відрізок прямої 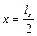. Причому, коли 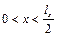функція 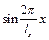– додатна, а при 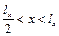– від’ємна. Тому, ліва і права половини мембрани прогинаються у різні боки і, відповідно, буде дві точки спучування. Це точки перетину прямої 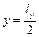з прямими 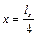і 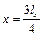(рис. 2.2б).

Представимо на рис. 2.2в і рис. 2.2г , відповідно, нормальні коливання 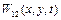і .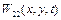

Звернемо увагу на одну важливу особливість коливання мембрани. При коливаннях струни кожній нормальній частоті відповідала одна власна форма коливань, яка цілком визначала форму струни. При коливаннях мембрани одній нормальній частоті може відповідати кілька власних форм. Такі ситуації виникають, коли відношення сторін мембрани дорівнює цілим числам. Наприклад, 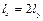, тоді

.

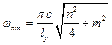Звідси маємо 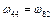, і таких ситуації можна відшукати безліч. Тому про це слід пам’ятати при розв’язанні інженерної задачі експериментального визначення власних форм коливань.

а	б
в	г
рис. 2.2