Вільні поперечні коливання струни

Виведемо диференціальне рівняння, що описує вільні коливання струни. Для цього розглянемо струну, що закріплена в точках А і В (рис.4.25а).

Початковий натяг струни позначимо через Т. Будемо вважати відхилення елемента струни маси dm від початкового горизонтального положення незначним, а зміною натягу Т при цьому нехтуємо, тобто Т=const. Довжина струни l.

Враховуючи, що при відхиленні всі точки струни знаходяться в площині Оху, розглянемо елемент струни маси dm з координатами

a)	б)
рис.4.25

х і х₁=х+dх. Проведемо дотичні до струни в початковій та кінцевій точках елементу; кути нахилу дотичних з віссю х будуть відповідно α і α₁ (рис.4.25б). Враховуючи те, що відхилення елемента струни від горизонтального положення малі, кути також вважаємо малими.

Складова натягу струни по осі Оу в точці х має вигляд

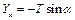, (4.42)

а в точці х₁=х+dх

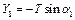. (4.43)

Якщо кути α і α₁ малі, то

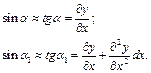(4.44)

Результуючий натяг ΔY, що діє на елемент струни рівний

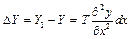, (4.45)

Для того, щоб знайти рівняння руху елемента струни, необхідно у відповідності з принципом 'Аламбера, ΔY прирівняти силі інерції елемента, що дорівнює 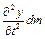. Таким чином,

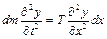, (4.46)

де 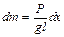, Р – вага струни.

Запишемо рівняння (4.46) у наступному вигляді

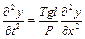. (4.47)

позначивши 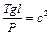, отримаємо диференціальне рівняння поперечних коливань натягнутої струни

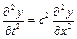. (4.48)

Будемо шукати розв'язок рівняння (4.48) у вигляді

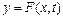. (4.49)

Ця функція повинна задовольняти наступним умовам:

1) диференціальному рівнянню (4.48);

2) граничним умовам, тобто умовам в точка х=0 і х=l, а саме:

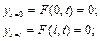(4.50)

3) початковим умовам, тобто:

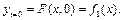(4.51)

Функція 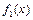задає форму всієї струни в початковий момент. Крім того, необхідно задати першу похідну по t при t=0.

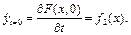(4.52)

Умова (4.52) означає, що в початковий момент всі точки струни мають задану швидкість, в тому числі можуть знаходитись в стані спокою.

Розв'язок рівняння (4.48), у відповідності з методом Фур'є, шукаємо у вигляді добутку двох функцій

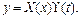(4.53)

Продиференціювавши вираз (4.53) по х і t, маємо

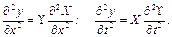(4.54)

Після підстановки (4.54) в (4.48) отримаємо

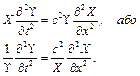(4.55)

Прирівнюючи ліву і праву частини до однієї і тієї ж постійної величини -k², матимемо два рівняння

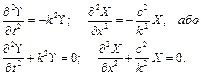(4.56)

Частинні розв'язки цих однорідних рівнянь мають вигляд:

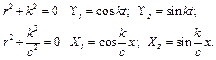(4.57)

В цьому легко переконатися, підставивши (4.57) в (4.56). Функція 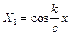не відповідає граничній умові 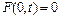, так як при х=0 в нуль не обертається і тому її виключаємо з подальшого розгляду.

Для того, щоб функція 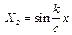оберталась в нуль при х=l необхідно, щоб kl=cnπ, де n – ціле число. Рівність

kl=cnπ (4.58)

називається рівнянням власних частот (або рівнянням періодів) струни.

З (4.58) випливає

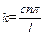. (4.59)

Тепер маємо два частинних розв'язки рівняння (4.58)

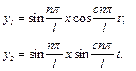(4.60)

Помноживши кожне з рівнянь (4.60) на невизначені коефіцієнти А_n та В_n, і склавши їх, отримаємо загальний розв'язок рівняння (4.48) у вигляді:

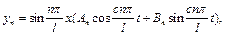(4.61)

або, позначивши 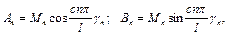де - де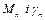які нові коефіцієнти, отримаємо

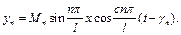(4.62)

Вираз (4.62) характеризує періодичний коливальний рух струни з круговою частотою

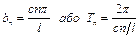, (4.63)

а частота в Гц дорівнює

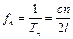. (4.64)

Повернемось до функції Х₂ (див.4.57)

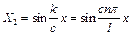(4.65)

і знайдемо перші три форми коливань струни (n=1, n=2, n=3).

На рис.4.26 вони представлені графічно

a)	б)	в)
рис.4.26

Характер руху струни залежить від початкових умов. Наприклад, якщо при t=0 струна мала форму першої кривої (рис.4.26а) і всі її точки були в спокої ( 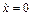), то вона буде надалі коливатись тільки з основною частотою (в основному тоні). Якщо ж початкова форма струни інша, то, крім основного тону з'являться і обертони, так як коливання струни будуть являти собою сукупність накладених один на одний окремих коливань. Рівняння руху струни (4.61) набуде в цьому випадку вигляду

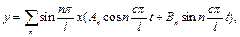(4.66)

Для остаточного розв'язку задачі необхідно з початкових умов (4.51) і (4.52) знайти 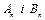рівняння (4.66). З умови (4.51) випливає

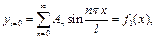(4.67)

а з умови (4.52)

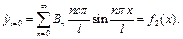(4.68)

Тут 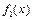і 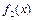- функції, що наперед задані в інтервалі [0,l].