Підставимо (4.5) в друге рівняння системи (4.17)

<42 43 444546 47 48 >

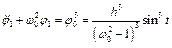. (4.20)

Так як за формулою пониження степеня 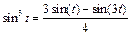, то (4.20) прийме вид

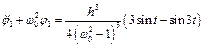. (4.21)

Загальний розв'зок рівняння (4.21) складається з суми розв'язків однорідного рівняння

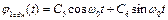, (4.22)

та частинного розв'язку, що шукається у виді

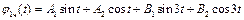. (4.23)

Знайшовши 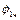та 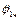, підставимо їх разом з (4.23) в рівняння (4.21), тоді отримаємо

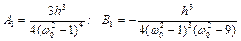Загальний розв'язок рівняння (4.21) має вигляд

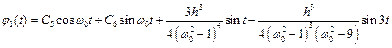. (4.24)

Умови періодичності виражаються подібними однорідними рівняннями

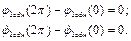
Умови періодичності для всіх функцій 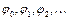будуть однакові. Таким чином, С₅=0, С₆=0 і тоді

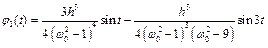Зупиняючись на першому наближенні для х(t), отримаємо

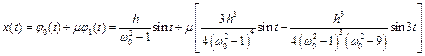Цей розв'язок при досить малому μ наближається до φ₀(t), обертаючись в нього при μ=0.

В данному випадку лінеаризація системи можлива, якщо визначник Δ≠0 (див. систему (*)). Тобто це і є, свого роду, критерій допустимості лінеаризації нелінійної системи.

II. Метод Крилова

Розглянемо другий приклад нелінійного диференціального рівняння другого порядку, що описує рух автономної системи методом Крилова.

Нехай рівняння має вид

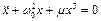. (4.25)

Розв'язок цього рівняння шукаємо у вигляді

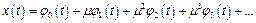(4.26)

Крім того, будемо шукати квадрат власної частоти також у вигляді ряду:

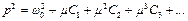, (4.27)

де С₁, С₂, С₃ – деякі шукані константи.

Підставимо (4.26) і (4.27) в (4.25) і отримаємо

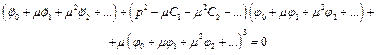
Побудуємо диференціальне рівняння за степенями малого параметра m.

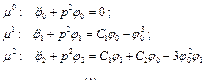(4.28)

Розв'язок системи рівнянь (4.28) шукаємо при наступних початкових умовах для x(t): t=0, , ,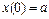

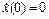або , ,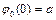

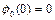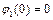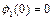, , (4.29)

, ,

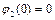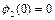Розглянемо перше рівняння системи (4.28)

. ( )

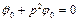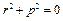Тоді .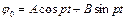

Підставивши початкові умови (4.29), знайдемо А=а, В=0. Остаточно

φ₀ = а cospt. (4.30)

Цей розв'язок підставимо у друге рівняння системи (4.28)

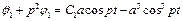. (4.31)

Скориставшись тим, що 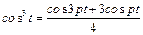, отримаємо (4.31) у вигляді

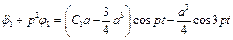. (4.32)

Для того, щоб не отримати "псевдо резонанс" в системі необхідно покласти

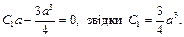
Після цього рівняння (4.32) матиме вигляд

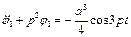. (4.33)

Знайдемо частинний розв’язок (4.33)

.

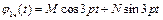Знайшовши 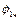, 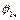і підставивши разом з 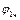у вихідне рівняння (4.33), отримаємо

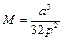; N=0.

Остаточно

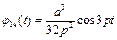. (4.34)

Розв'язок однорідного рівняння для (4.33) має вигляд

.

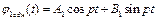Запишемо загальний розв'язок рівняння (4.33)

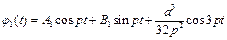. (4.35)

При нульових початкових умовах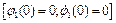

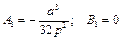і

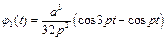. (4.36)

Таким чином, розв'язок нелінійного рівняння (4.25) в першому наближенні має вигляд

,

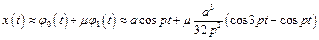де 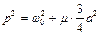(4.37)

Частота власних коливань збільшується при збільшенні амплітуди.

Для того, щоб отримати друге наближення, необхідно підставити 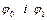в третє рівняння системи (4.28) і так далі.

<42 43 444546 47 48 >

Дата добавления: 2020-08-31; просмотров: 408;