Вільні коливання в електричному контурі з нелінійною ємністю
Розглянемо коливальний контур (рис.1.8), в якому немає лінійної залежності напруги на ємності від заряду. Такими властивостями володіють конденсатори з сегнетоелектриків. Згідно закона Кирхгофа
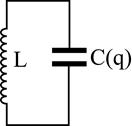
Рисунок 1.8 – Електричний контур

де 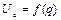 – напруга на обкладинках конденсатора,
– напруга на обкладинках конденсатора,
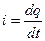 – струм в системі. Тоді для зміни заряду маємо рівняння
– струм в системі. Тоді для зміни заряду маємо рівняння
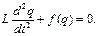 (1.21)
(1.21)
Задамося залежністю вольт-кулоновської характеристики (рис.1.9) конденсаторів з сегнетоелектриків, що часто зустрічається у формі кубічної параболи виду
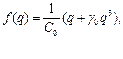 (1.22)
(1.22)
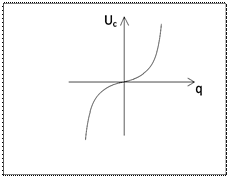
Рисунок 1.9 – Вольт-кулонівська характеристика конденсатора з сегнетоелектриків
де 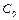 – ємність конденсатора при
– ємність конденсатора при 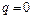 ,
,
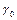 – коефіцієнт нелінійності.
– коефіцієнт нелінійності.
Рівняння (1.21) приймає вигляд:
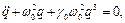 (1.23)
(1.23)
де 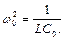
Це рівняння відноситься до вже розглянутого раніше неліній-ного рівняння типу (1.7), тому його наближене рішення можна записати відразу
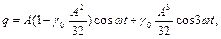 (1.24)
(1.24)
де
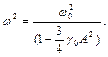 (1.25)
(1.25)
У цьому випадку ми так само зустрічаємося з неізохронністю коливань і явищем ангармонізму. Графік (рис.1.7) залежності частоти від амплітуди відповідає верхній кривій. Звернемо увагу на ту обставину, що при 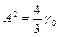
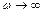 . Цей результат свідчить про недостатність використання тільки першого наближення методу. Більше того, якщо навіть вважати апроксимацію
. Цей результат свідчить про недостатність використання тільки першого наближення методу. Більше того, якщо навіть вважати апроксимацію  точною, то при великих амплітудах коливань перше наближення (1.24) і залежність (1.25) стають непридатними. У цьому також виявляється обмеженість методу послідовних наближень.
точною, то при великих амплітудах коливань перше наближення (1.24) і залежність (1.25) стають непридатними. У цьому також виявляється обмеженість методу послідовних наближень.
Метод ізоклин. Фазовий портрет можна побудувати й іншим методом - методом ізоклин. Ізоклинами на фазовій площині називаються лінії, на яких нахил фазових траєкторій однаковий. Продемонструємо побудову фазового портрету методом ізоклин на прикладі нелінійного контуру.
Введемо безрозмірний заряд 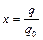 , безрозмірний час
, безрозмірний час 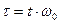 , а також позначення
, а також позначення 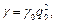
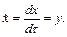
Тоді рівняння (1.23) в фазових змінних прийме вигляд:
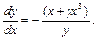 (1.26)
(1.26)
Рівняння сімейства ізоклин запишуться у вигляді:  , де
, де 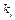 – довільні числа, або
– довільні числа, або
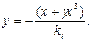 (1.27)
(1.27)

Рисунок 1.10 – Фазовий портрет контуру з нелінійною ємністю
Бачимо, що ізоклинами є кубічні параболи з різними коефіцієнтами  . Виняток становлять дві ізоклини: нульова
. Виняток становлять дві ізоклини: нульова 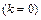 збігається з віссю координат
збігається з віссю координат 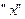 і ізоклина нескінченності
і ізоклина нескінченності 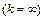 збігається з віссю координат
збігається з віссю координат 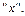 Ізоклини і фазовий портрет зображені на
Ізоклини і фазовий портрет зображені на
рис. 1.10.
Дата добавления: 2020-08-31; просмотров: 684;











