Принцип Лагранжа (Принцип можливих переміщень; Загальне рівняння статики)

Найзагальніші методи розв’язування задач механіки ґрунтуються на загальному принципі аналітичної статики, який називається принципом можливих переміщень, або принципом Лагранжа. Об’єднавши його з відомим принципом Даламбера, Лагранж дістав загальне рівняння динаміки, з якого як наслідок випливають основні диференціальні рівняння руху системи.

Принцип можливих переміщень є наслідком визначення можливих переміщень і деяких властивостей в’язей.

Принцип можливих переміщень

Якщо система матеріальних точок з ідеальними в’язями перебуває в рівновазі, то сума робіт активних сил, прикладених до точок системи, на можливих переміщеннях або дорівнює нулю, або від’ємна .

рис.3.6

Розглянемо систему n точок (рис.3.6) з ідеальними в’язями, яка перебуває в рівновазі. У рівновазі перебуває і кожна точка системи. Тому, користуючись аксіомою про звільнення від в’язей, маємо

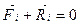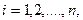; (a)

де 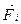- рівнодійна активних сил, прикладених до 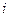- тої точки системи; 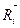рівнодійна реакцій ідеальних в’язей, прикладених до цієї самої точки.

Надамо точкам системи можливих переміщень 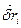і обчислимо роботу, яку виконують активні сили і реакції в’язей на цих переміщеннях:

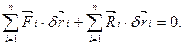(b)

Користуючись умовою (4.1) , дістаємо

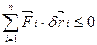. (3.4)

Знак нерівності відповідає, як і раніше, наявності серед в’язей нестримуючих. Довели необхідність виконання умови (3.4) для рівноваги системи. Доведемо її достатність.

Припустимо, що система зі стану рівноваги починає рухатися. За теоремою про зміну кінетичної енергії системи робота, виконана діючими на систему силами, на дійсних переміщеннях додатна. Вважатимемо в’язі, накладені на точки системи, стаціонарними. Тоді дійсні переміщення збігаються з одним із можливих. Отже, це і буде робота, яку виконують активні сили на можливих переміщеннях. Але це твердження суперечить умові (3.4), тобто невірне.

Принцип повністю доведено.

Умовимося розглядати тільки такі можливі переміщення, які не звільняють систему від в’язей. Співвідношення (3.4) набуває вигляду

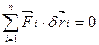(3.5)

і називається загальним рівнянням статики. Цей термін можна пояснити тим, що з нього легко дістати умови рівноваги вільного твердого тіла і всі можливі умови рівноваги системи тіл.

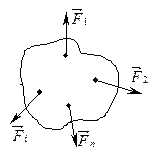
рис. 3.7

Розглянемо вільне тверде тіло (рис.3.7), на яке діють сили 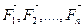. Якщо тіло невільне, скористаємось аксіомою про звільнення від в’язей і реакції в’язей приєднаємо до активних сил.

Надамо тілу певного можливого переміщення і обчислимо елементарну роботу всіх діючих сил на цьому переміщенні. Згідно з теоремою про роботу сил, що діють на абсолютно тверде тіло, ця робота дорівнює роботі, виконаній головним вектором системи сил на переміщенні полюса, і роботі головного моменту відносно полюса на обертальному переміщенні навколо полюса:

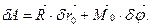(c)

Полюс беремо в довільній точці О. На підставі (3.5) вираз (c) набуває вигляду

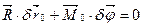(d)

Можливе переміщення полюса 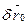і обертальне переміщення навколо полюса 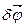- незалежні. Нехай 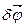=0, .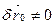

Тоді з (m) маємо .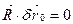

Ця умова здійснюється для всіх довільних 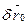лише тоді, коли

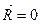. (e)

Аналогічно можна довести , що

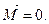(f)

Рівності (e) та (f) – відомі умови рівноваги вільного твердого тіла.

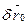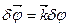Аналогічно можна знайти умови рівноваги невільного твердого тіла. Розглянемо, наприклад, тверде тіло, що має дві нерухомі точки, нерухому вісь. Візьмемо полюс на цій осі. Тоді =0, а , де 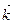- орт осі обертання.

Рівняння (d) набуває вигляду

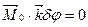. (g)

Співвідношення (g) повинно бути справедливим при довільному 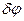. Отже,

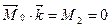(h)

Рівність (h) – відома умова рівноваги тіла з нерухомою віссю.