Уравнения фильтра Калмана

Пусть наблюдается некоторый дискретный сигнал 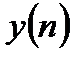, который связан с полезным сигналом 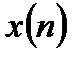уравнением наблюдения:

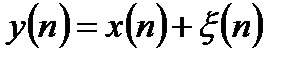, (13.30)

где 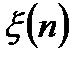- дискретный белый гауссовский шум наблюдения.

Разностное уравнение для случайногополезного сигнала имеет следующий вид:

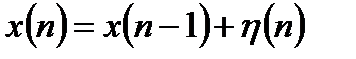, (13.31)

где 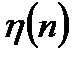- дискретный белый шум.

В этом случае невозможно получить уравнения оптимальной фильтрации путем математических преобразований уравнений фильтрации, полученных методом МНК и необходимо использовать уравнения фильтра Калмана.

Уравнения фильтра Калмана совпадают по форме с алгоритмами фильтрации неслучайного постоянного сигнала:

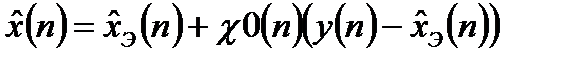, (13.32)

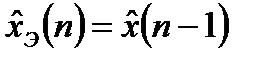. (13.33)

Однако коэффициент фильтрации в этом случае отличается и описывается следующим рекуррентным выражением, полученным Калманом:

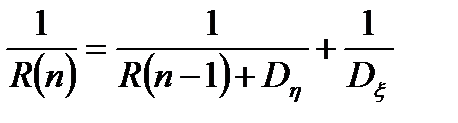, (13.34)

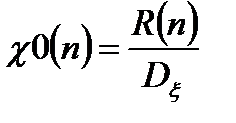, (13.35)

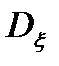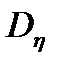где и - дисперсии дискретных случайных процессов шума наблюдения 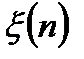и формирующего шума .

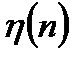Коэффициент фильтрации может быть рассчитан заранее и не зависит от входного сигнала.

После окончания окончания переходного процесса коэффициент фильтрации является постоянной ненулевой величиной.

Рисунок 13.6 – структурная схема рекуррентной оптимальной линейной фильтрации постоянного сигнала и фильтра Калмана

1. Сосулин Ю.Г. Теоретические основы радиолокации и радионавигации: Учеб. пособие для вузов. – М.: Радио и связь, 1992. – 304 с.: ил.

2. Честаховский В.П. Автоматизированные системы управления войск противовоздушной обороны сухопутных войск. Часть 1. Основы построения автоматизированных систем управления. Учебник. – Киев: Издательство ВА ПВО СВ, 1977. – 395 с.

3. Васильев К.К. Методы обработки сигналов: Учебное пособие. – Ульяновск, 2001. – 80 с. (с. 47).