Оптимальная линейная фильтрация неслучайного постоянного полезного сигнала

Пусть разностное уравнение для полезного сигнала имеет следующий вид:

. (13.5)

Таким образом, неизвестный полезный сигнал является неслучайным и постоянным. Такому разностному уравнению соответствует модель полезного сигнала в виде полинома нулевого порядка:

,

где 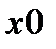- некоторый параметр неслучайного постоянного полезного сигнала (начальное значение).

В этом случае оптимальная оценка сигнала на фоне дискретного белого шума методом МНК определяется выражением для оценки математического ожидания наблюдаемого случайного сигнала:

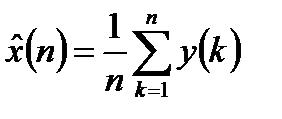. (13.6)

В соответствии с разностным уравнением для полезного сигнала (13.5) сумму квадратов ошибки можно записать в следующем виде:

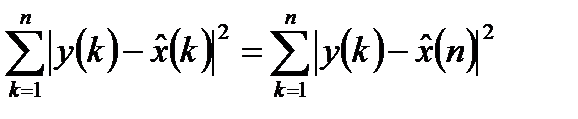. (13.7)

Оптимальной оценкой полезного сигнала будет оценка, минимизирующая сумму квадратов (13.7) или обращающая в ноль ее производную по оцениваемому параметру:

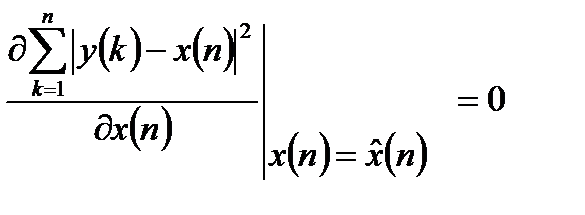(13.8)

или

,

.

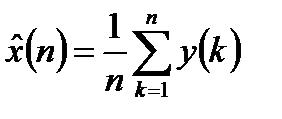Для получения рекуррентного оптимального дискретного фильтра проведем математические преобразования оптимальной оценки методом МНК.

. (13.9)

Первое слагаемое в выражении (13.9) включает в себя оптимальную оценку полезного сигнала в предыдущий момент времени :

. (13.10)

С учетом выражения (13.10) выражение (13.9) можно записать следующим образом:

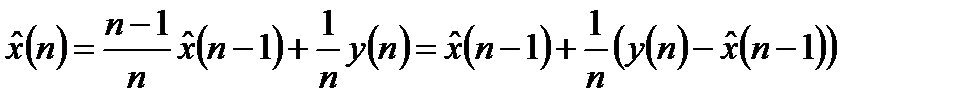. (13.11)

Таким образом, получено рекуррентное выражение для оптимальной оценки дискретного постоянного полезного сигнала:

. (13.12)

Выражение (13.12) может быть также записано и в следующем виде:

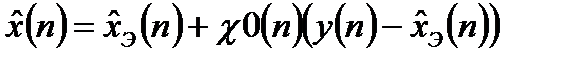, (13.13)

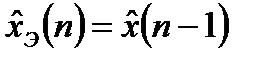, (13.14)

,

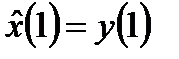где 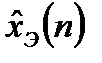- экстраполированное (предсказанное) значение измеряемого дискретного сигнала;

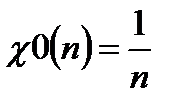- коэффициент фильтрации по положению постоянного сигнала.

Структурная схема оптимального линейного дискретного фильтра постоянного сигнала имеет следующий вид: рисунок 13.1.

Рисунок 13.1 – структурная схема рекуррентной оптимальной линейной фильтрации постоянного сигнала

В соответствии с рисунком 13.1 оптимальный реккурентный фильтр для постоянного сигнала представляет собой дискретную следящую систему с переменным коэффициентом фильтрации и цифровым интегратором.

Переменный коэффициент фильтрации в данном случае стремится к нулю с течением времени.