Синтез цифровой следящей системы для прототипа с первым порядком астатизма

Будем полагать, что передаточная функция разомкнутой аналоговой следящей системы содержит один интегратор:

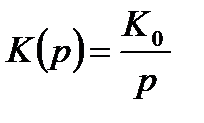. (14.7)

Передаточная функция замкнутой следящей системы имеет следующий вид:

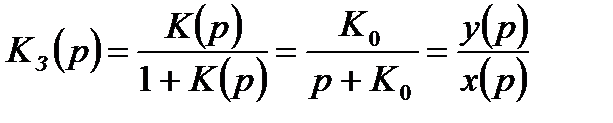. (14.8)

Характеристический полином следящей системы запишется следующим образом:

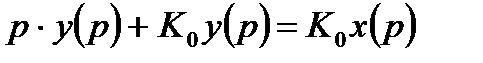(14.9)

или

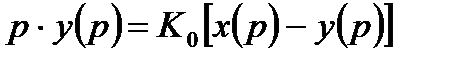. (14.10)

Дифференциальное уравнение, описывающее работу следящей системы имеет вид:

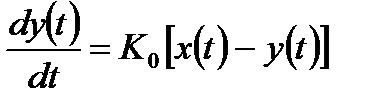. (14.11)

Переход от дифференциального уравнения к разностному уравнению осуществляется следующим образом:

. (14.12)

Для получения рекуррентного вида разностного уравнения выразим текущее значение выходного сигнала через его предыдущие значения:

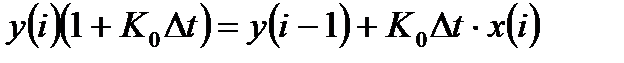
или

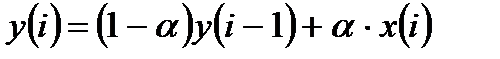, (14.13)

где .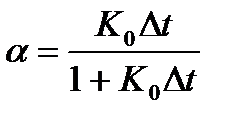

Преобразуем полученный рекуррентный алгоритм к виду, содержащему экстраполированное значение выходного сигнала и выход дискриминатора:

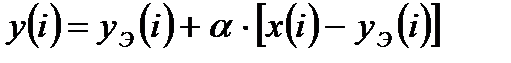, (14.14)

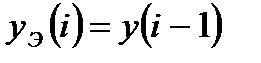. (14.15)

Полученный алгоритм цифровой фильтрации также называется 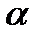- фильтром. Коэффициент фильтрации 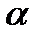может быть получен пересчетом коэффициента преобразования 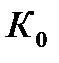разомкнутой аналоговой следящей системы.

Алгоритму соответствует структурная схема, приведенная на рисунке 14.2.

Рисунок 14.2 – структурная схема 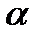- фильтра

14.4. Синтез цифровой следящей системы для прототипа со вторым порядком астатизма (α-β фильтр)

Будем полагать, что передаточная функция разомкнутой аналоговой следящей системы содержит два интегратора:

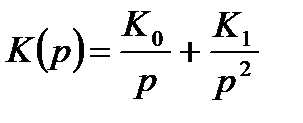. (14.16)

Передаточная функция замкнутой следящей системы имеет следующий вид:

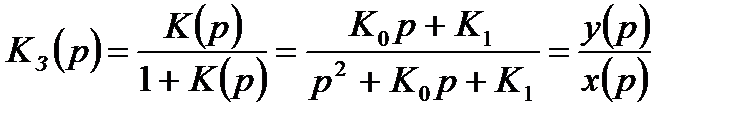. (14.17)

Характеристический полином следящей системы запишется следующим образом:

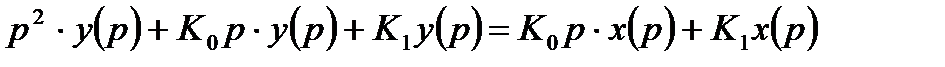(14.18)

или

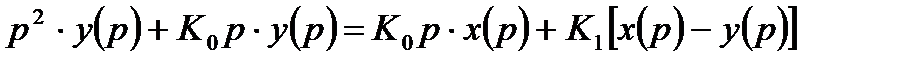. (14.19)

Дифференциальное уравнение, описывающее работу следящей системы в соответствии с выражением (14.19) примет вид:

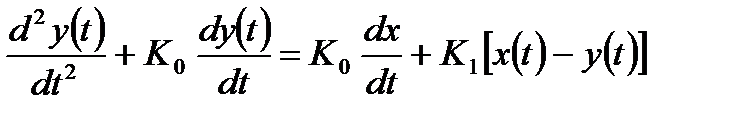. (14.20)

Переход от дифференциального уравнения к разностному уравнению осуществляется следующим образом:

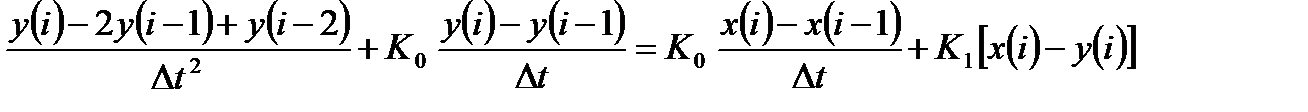. (14.21)

Для получения рекуррентного вида разностного уравнения выразим текущее значение выходного сигнала через его предыдущие значения:

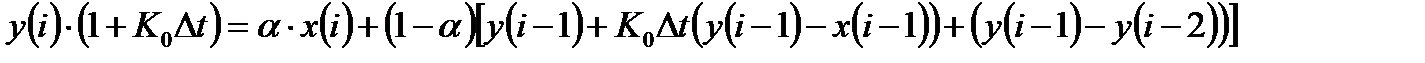, (14.22)

где .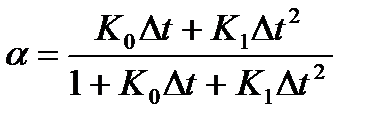

Преобразуем полученный рекуррентный алгоритм к конечному виду, содержащему формирование экстраполированного значения выходного сигнала и рассогласования между входным сигналом и экстраполированным значением выходного сигнала:

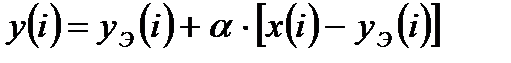, (14.23)

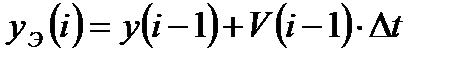, (14.24)

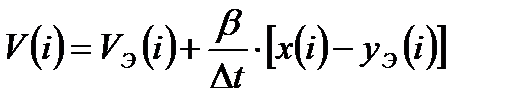, (14.25)

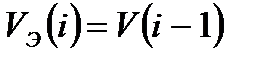, (14.26)

где .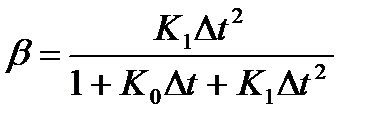

Полученный алгоритм цифровой фильтрации также называется 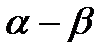- фильтром.

Коэффициенты фильтраци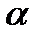и и 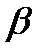могут быть получены пересчетом коэффициентов преобразования 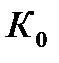и 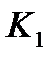разомкнутой аналоговой следящей системы с учетом интервала дискретизации .

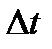Алгоритму фильтрации соответствует структурная схема, приведенная на рисунке 14.3.

Рисунок 14.3 – структурная схема 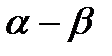- фильтра

Литература

1. Охрименко А.Е. Основы обработки и передачи информации. Минск: Минское ВИЗРУ. 1990. 180 с.

2. Глинченко А.С. Цифровая обработка сигналов: в 2 ч. Ч.1. Красноярск: Изд-во КГТУ. 2001. 199 с. (п. 6.4.1, п. 6.4.2).