Кратковременное дискретное преобразование Фурье.

В задачах спектрального анализа нестационарных сигналов используется кратковременное преобразование Фурье (КПФ):

, (12.3)

где w[n] – весовая последовательность.

КПФ зависит от двух параметров: целочисленного временного индекса n и значения непрерывной частоты w. КПФ является периодической функцией частоты с периодом 2p. Модуль 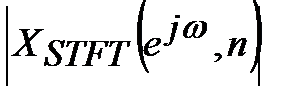часто называют спектрограммой.

Дискретизация КПФ в частотной области в точках 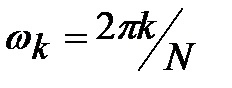приводит к дискретному кратковременному преобразованию Фурье, которое можно трактовать как R-точечное ДПФ функции (x[n-m]w[m]), N ³ R:

,

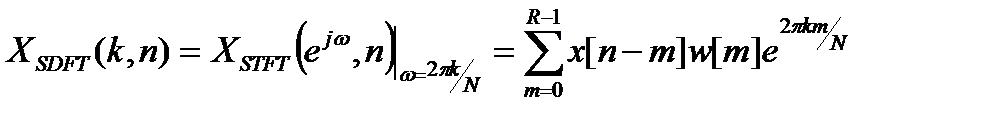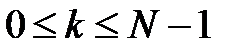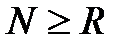, . (12.4)

При равенстве размеров ДПФ и массива анализируемых данных N = R получаем взвешенное ДПФ:

. (12.5)

Фактически при данном преобразовании временной интервал сигнала дееюнется на подинтервалы и преобразование выполняется последовательно для каждого подинтервала в отдельности. Тем самым осуществляется переход к частотно-временному представлению сигналов, при этом в пределах каждого подинтервала сигнал «считается» стационарным.

Разрешающая способность локализации определяется принципом неопределенности Гейзенберга, который гласит, что невозможно получить произвольно точное частотно-временное представление сигнала. При ширине оконной функции, равной , частотная разрешающая способность определяется значением 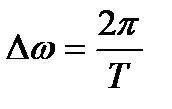. При требуемой величине частотного разрешения 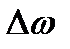соответственно ширина оконной функции должна быть равна 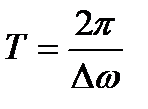. Чем уже окно, тем лучше временное разрешение, но хуже частотное, и наоборот. Для оконного преобразования Фурье эти ограничения являются принципиальными.

Узкое окно обеспечивает лучшее временное разрешение и четкую фиксацию границ интервалов, но широкие пики частот в пределах интервалов. Широкое окно напротив – четко отмечает частоты интервалов, но с перекрытием границ временных интервалов. При решении практических задач приходится выбирать окно для анализа всего сигнала, тогда как разные его участки могут требовать применения разных окон. Если сигнал состоит из далеко отстоящих друг от друга частотных компонент, то можно пожертвовать спектральным разрешением в пользу временного, и наоборот.