Дискретные вейвлет-преобразования.

12.3.1. Общие сведения о вейвлет-преобразованиях.

Вейвлетное преобразование сигналов является обобщением спектрального анализа, типичный представитель которого – классическое преобразование Фурье.

Вейвлет-преобразования (WT) подразделяют на дискретное (DWT) и непрерывное (CWT). DWT используется для преобразований и кодирования сигналов, CWT – для анализа сигналов.

В вейвлет-анализе роль базисных функций играют функции особого рода, называемые вейвлетами. Термин «вейвлет» (wavelet) в переводе с английского означает «маленькая (короткая) волна». Вейвлеты – это обобщенное название семейств дтематических функций определенной формы, которые локальны во времени и по частоте, и в которых все функции получаются из одной базовой (порождающей) функции посредством ее сдвигов и растяжений по оси времени.

Вейвлет-преобразования рассматривают анализируемые временные функции в терминах колебаний, локализованных по времени и частоте.

Отличительной особенностью вейвлет-анализа является то, что в нем можно использовать семейства функций, реализующих различные варианты соотношения неопределенности. Соответственно, исследователь имеет возможность гибкого выбора между ними и применения тех вейвлетных функций, которые наиболее эффективно решают поставленные задачи.

Основная область применения вейвлетных преобразований – анализ и обработка сигналов и функций, нестационарных во времени, когда результаты анализа должны содержать не только частотную характеристику сигнала (распределение энергии сигнала по частотным составляющим), но и сведения о локальных координатах, на которых проявляют себя те или иные группы частотных составляющих или на которых происходят быстрые изменения частотных составляющих сигнала.

На рисунке 12.1 анализируемый сигнал состоит из двух модулированных деесианов. Преобразование вейвлетом Морлета четко показывает их пространственную и частотную локализацию, в то время как спектр Фурье дает только частотную локализацию.

Одна из главных и особенно плодотворных идей вейвлетного представления сигналов заключается в разделении функций приближения к сигналу на две группы: аппроксимирующую – грубую, с достаточно медленной временной динамикой изменений, и детализирующую – с локальной и быстрой динамикой изменений на фоне плавной динамики, с последующим их дроблением и детализацией на других уровнях декомпозиции сигналов. Это возможно как во временной, так и в частотной областях представления сигналов вейвлетами.

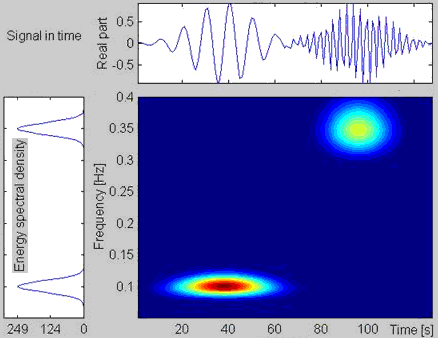Рисунок

Рисунок 12.1 – вейвлет-преобразование сигнала

12.3.2. Базисные функции вейвлет-преобразований.

Вейвлеты имеют вид коротких волновых пакетов с нулевым средним дееюнем, локализованных по оси аргументов, инвариантных к сдвигу и линейных к операции масштабирования. По локализации во временном и частотном представлении вейвлеты занимают промежуточное положение между гармоническими функциями, локализованными по частоте, и функцией Дирака, локализованной во времени.

Базисная функция вейвлет представляет собой некоторое «короткое» колебание. Причем понятие частоты спектрального анализа заменено масштабом, и для перекрытия «короткими волнами» всей временной оси введен сдвиг функций во времени. Базис вейвлетов – это временные функции типа:

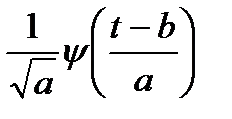, (12.6)

где b – сдвиг;

а – масштаб.

Функция 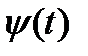должна иметь нулевую площадь. Фурье-преобразование таких функций равно нулю на нулевой частоте 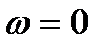и имеет вид полосового фильтра. Различные значениях масштабного параметра 'a' это соответствуют набору полосовых фильтров. Семейства вейвлетов во временной или частотной области используются для представления сигналов и функций в виде суперпозиций вейвлетов на разных масштабных уровнях декомпозиции (разложения) сигналов.

Следующая функция

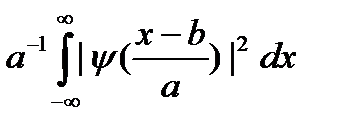
не зависит от параметров 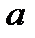и 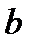. Вектор, заданный функцией 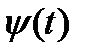, имеет постоянную длину в пространстве:

.

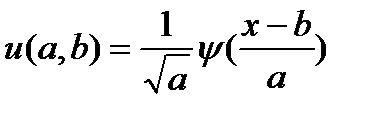На практике, в качестве базовой функции часто используют функцию

,

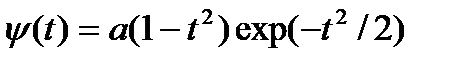называемую мексиканской шляпой.

12.3.3. Непрерывное вейвлет-преобразование.

Пусть имеется функция и некоторая функция 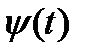- базисная функция. Непрерывное вейвлет-преобразование описывается выражением вида:

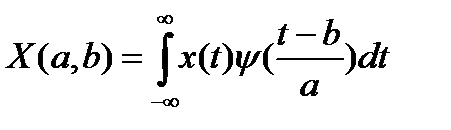. (12.7)

Если базисная функция описывается выражением:

,

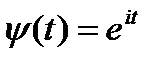то в результате имеется обычное преобразование Фурье (в этом случае параметр 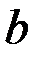не используется).

Для перекрытия функцией вейвлета всей временной оси пространства используется операция сдвига (смещения по временной оси): 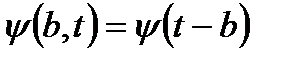, где значение b для НВП является величиной непрерывной. Для перекрытия всего частотного диапазона используется операция временного масштабирования вейвлета с непрерывным изменением независимой переменной: 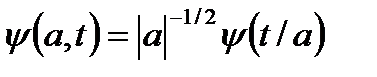. Таким образом, путем сдвига по независимой переменной (t-b) вейвлет имеет возможность перемещаться по всей числовой оси произвольного сигнала, а путем изменения масштабной переменной 'а' (в фиксированной точке (t-b) оси) «просматривать» частотный спектр сигнала по определенному интервалу окрестностей этой точки.

Таким образом, непрерывное вейвлет-преобразование представляет собой разложение сигнала по всем возможным сдвигам и сжатиям/растяжениям некоторой локализованной финитной функции – вейвлета. При этом переменная 'a' определяет масштаб вейвлета и эквивалентна частоте в преобразованиях Фурье, а переменная 'b' – сдвиг вейвлета по сигналу от начальной точки в области его определения, шкала которого повторяет временную шкалу анализируемого сигнала.

Понятие масштаба ВП имеет аналогию с масштабом географических карт. Большие значения масштаба соответствуют глобальному представлению сигнала, а низкие значения масштаба позволяют различить детали. В терминах частоты низкие частоты соответствуют глобальной информации о сигнале, а высокие частоты – детальной информации и особенностям, которые имеют малую протяженность, т.е. масштаб вейвлета, как единица шкалы частотно-временного представления сигналов, обратен частоте. Масштабирование, как математическая операция, расширяет или сжимает сигнал. Большие значения масштабов соответствуют расширениям сигнала, а малые значения – сжатым версиям. В определении вейвлета коэффициент масштаба а стоит в знаменателе. Соответственно, а > 1 расширяет сигнал, а < 1 сжимает его.

12.3.4. Дискретное вейвлет-преобразование.

В принципе, при обработке данных на ПК может выполняться дискретизированная версия непрерывного вейвлет-преобразования с заданием дискретных значений параметров (a, b) вейвлетов с произвольным шагом a и b. В результате получается избыточное количество коэффициентов, намного превосходящее число отсчетов исходного сигнала, которое не требуется для реконструкции сигналов.

Дискретное вейвлет-преобразование (ДВП) обеспечивает достаточно информации, как для анализа сигнала, так и для его синтеза, являясь вместе с тем экономным по числу операций и по требуемой памяти. ДВП оперирует с дискретными значениями параметров а и b, которые задаются, как правило, в виде степенных функций:

,

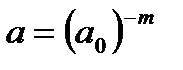(12.8)

,

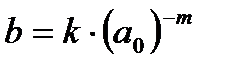где ;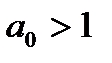

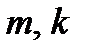- целые числа;

- параметр масштаба;

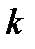- параметр сдвига.

Базис пространства в дискретном представлении:

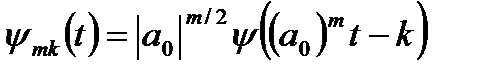. (12.9)

Вейвлет-коэффициенты прямого преобразования:

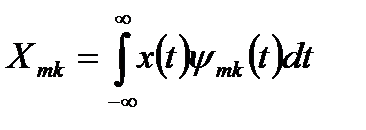. (12.10)

Значение 'a' может быть произвольным, но обычно принимается равным 2, при этом преобразование называется диадным вейвлет-преобразованием. Для диадного преобразования разработан быстрый алгоритм вычислений, аналогичный быстрому преобразованию Фурье, что предопределило его широкое использование при анализе массивов цифровых данных.

Обратное дискретное преобразование для непрерывных сигналов при нормированном ортогональном вейвлетном базисе пространства:

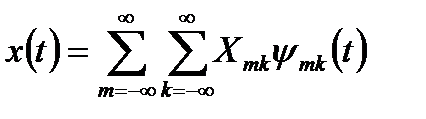. (12.11)

Число использованных вейвлетов по масштабному коэффициенту m задает уровень декомпозиции сигнала, при этом за нулевой уровень (m = 0) обычно принимается уровень максимального временного разрешения сигнала, т.е. сам сигнал, а последующие уровни (m < 0) образуют ниспадающее вейвлет-дерево. В программном обеспечении вычислений для исключения использования отрицательной нумерации по m знак 'минус' обычно переносится непосредственно в следующее представление базисных функций:

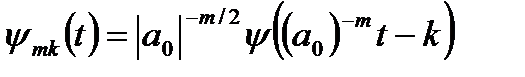. (12.12)

12.3.5. Частотно-временная локализация вейвлет-анализа.

Реальные сигналы, как правило, конечны. Частотный спектр сигналов обратно пропорционален их длительности. Соответственно, достаточно точный низкочастотный анализ сигнала должен производиться на больших интервалах его задания, а высокочастотный – на малых. Если частотный состав сигнала претерпевает существенные изменения на интервале его задания, то преобразование Фурье дает только усредненные данные частотного состава сигнала с постоянным частотным разрешением. Определенная частотно-временная локализация анализа создается дееюниием оконного преобразования Фурье, что дает семейства частотных спектров, локализованных во времени, но в пределах постоянной ширины окна оконной функции, а, следовательно, также с постоянным значением и частотного, и временного разрешения.

В отличие от оконного преобразования Фурье, вейвлет-преобразование, при аналогичных дискретных значениях сдвигов b, дает семейства спектров масштабных коэффициентов а сжатия-растяжения:

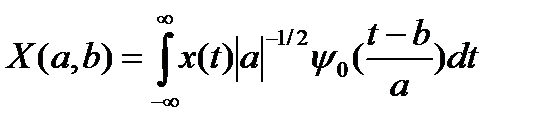. (12.13)

Если считать, что каждый вейвлет имеет определенную «ширину» своего временного окна, которому соответствует определенная «средняя» частота спектрального образа вейвлета, обратная его масштабному коэффициенту а, то семейства масштабных коэффициентов вейвлет-преобразования можно считать аналогичными семействам частотных спектров оконного преобразования Фурье, но с одним принципиальным отличием. Масштабные коэффициенты изменяют «ширину» вейвлетов и, соответственно, «среднюю» частоту их фурье-образов, а, следовательно, каждой частоте соответствует своя длительность временного окна анализа, и наоборот. Так малые значения параметра а, характеризующие быстрые составляющие в сигналах, соответствуют высоким частотам, а большие значения – низким частотам. За счёт изменения масштаба вейвлеты способны выявлять различия на разных частотах, а за счёт сдвига (параметр b) проанализировать свойства сигнала в разных точках на всём исследуемом временном интервале. Многоразмерное временное окно вейвлет-преобразования адаптировано для оптимального выявления и низкочастотных, и высокочастотных характеристики сигналов.

Таким образом, на высоких частотах лучше разрешение по времени, а на низких – по частоте. Для высокочастотной компоненты сигнала мы можем точнее указать ее временную позицию, а для низкочастотной – ее значение частоты.

Высокочастотная (мелкомасштабная) информация вычисляется на основе длых интервалов сигналов, а низкочастотная – на основе больших. Поскольку анализируемые сигналы всегда конечны, то при вычислении коэффициентов на границах задания сигнала область достоверности выходит за пределы сигнала, и для уменьшения погрешности вычислений сигнал дополняется заданием начальных и конечных условий.

12.3.6. Достоинства и недостатки вейвлет-анализа.

К достоинствам вейвлет-анализа можно отнести:

- вейвлетные преобразования обладают всеми достоинствами преобразований Фурье;

- вейвлетные базисы могут быть хорошо локализованными как по частоте, так и по времени;

- при выделении в сигналах хорошо локализованных разномасштабных процессов можно рассматривать только те масштабные уровни разложения, которые представляют интерес;

- вейвлетные базисы, в отличие от преобразования Фурье, имеют много разнообразных базовых функций, свойства которых ориентированы на решение различных задач.

Недостатком вейвлетных преобразований является их относительная сложность.

12.3.7. Свойства вейвлет-анализа.

Получение объективной информации о сигнале базируется на свойствах вейвлет-преобразования, общих для вейвлетов всех типов. Рассмотрим основные из этих свойств. Для обозначения операции вейвлет-преобразования произвольных функций х(t) будем применять индекс TW[x(t)].

Линейность.

TW[α·x₁(t)+β·x₂(t)] = α·TW[x₁(t)]+β·TW[x₂(t)].

Инвариантность относительно сдвига. Сдвиг сигнала во времени на t₀ приводит к сдвигу вейвлет-спектра также на t₀:

TW[x(t-t_o)] = X(a, b-t_o).

Инвариантность относительно масштабирования. Растяжение (сжатие) сигнала приводит к сжатию (растяжению) вейвлет-спектра сигнала:

TW[x(t/а_o)] = (1/а_о)·X(a/а_о,b/а_o).

Дифференцирование.

Dⁿ{TW[x(t)]}/dtⁿ = TW[dⁿ(x(t))/dtⁿ].

TW[dⁿ(x(t))/dtⁿ] = (-1)ⁿ x(t) [dⁿ(ψ(t))/dtⁿ] dt.

Безразлично, дифференцировать функцию или анализирующий вейвлет. Если деелизирующий вейвлет задан формулой, то это может быть очень полезным для деелиза сигналов. Проанализировать особенности высокого порядка или мелкомасштабные вариации сигнала x(t) с игнорированием крупномасштабных полиномиальных составляющих (тренда и регионального фона) можно дифференцированием нужного числа раз либо вейвлета, либо самого сигнала. Это свойство особенно полезно, когда сигнал задан дискретным рядом.

Аналог теоремы Парсевалядля ортогональных и биортогональных вейвлетов.

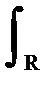x₁(t)·x₂*(t) = X_ψ^-1 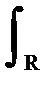a^-2 X(a,b) X*(a,b) da db.

Отсюда следует, что энергия сигнала может вычисляться через коэффициенты вейвлет-преобразования.

Литература

Основы цифровой обработки сигналов: учебное пособие / Ю.А. Брюханов, А.А. Приоров, В.И. Джиган, В.В. Хрящев; Яросл. Гос. ун-т им. П.Г. Демидова. – Ярославль: ЯрГУ, 2013. – 344 с. (с. 270)