Анализ магнитных цепей постоянного тока

Суть анализа сводится к определению основных параметров магнитных цепей: Н, Ф, В, I, S. При этом пользуются понятиями магнитодвижущей силы, закона полного тока, магнитного напряжения 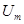и магнитного сопротивления .

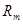Если по намагничивающей обмотке протекает ток I, то магнитодвижущей силой обмотки F называют произведение величины тока на число витков:

v (8.7)

Связь между магнитодвижущей силой F и напряженностью магнитного поля Н устанавливает закон полного тока:

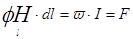(8.8)

При анализе магнитных цепей пользуются значением средней линии магнитопровода, поэтому

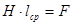(8.9)

Произведение

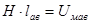(8.10)

называют магнитным напряжением участка цепи длиной ав.

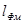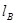Если магнитная цепь содержит два неоднородных участка длиной и , то

или

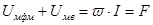(8.11)

Таким образом алгебраическая сумма магнитных напряжений на участках цепи равна магнитодвижущей силе обмотки. Выражение (8.11) представляет собой второй закон Кирхгофа для магнитной цепи.

Аналогично первого закона Кирхгофа является теорема Гауса: поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

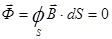(8.12)

Рассмотрим выражение для магнитногонапряжения

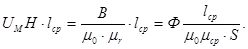
Обозначим выражение

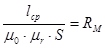
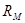называется магнитным сопротивлением.

Тогда

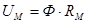(8.13)

Равенство (8.13) представляет собой закон Ома для магнитной цепи.

Если основной характеристикой электрической цепи является вольт-амперная характеристика, то для магнитной цепи - это ампер-веберная характеристика - зависимость между магнитным потоком и намагничивающим током 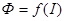(рис.8.6).

На рис. 8.6 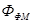- поток в ферромагнитном материале, 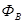- поток в воздушном зазоре, 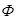_å - результирующий поток.

На практике используется зависимость 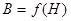, так как Н пропорциональна намагничивающему току I, а В пропорциональна магнитному потоку Ф.