Дискретные автоматические системы регулирования
3.10.1. Понятия о дискретных АСР и их классификация
В непрерывных системах существуют только непрерывные сигналы, являющиеся непрерывными функциями времени. В дискретных АСР сигнал изменяется во времени дискретно, скачками.
Преобразование непрерывного сигнала в дискретный называется квантованием сигнала. Существует два основных вида квантования: по уровню и по времени.
В соответствии с видами квантования АСР дискретного действия делятся на три типа: релейные, импульсные и цифровые.
В этом разделе подробнее рассмотрим лишь релейные АСР.
3.10.2. Классификация релейных АСР
Большинство релейных АСР можно представить, как показано на рис. 3.37. Здесь НП – непрерывная часть системы, а РЭ – релейный элемент.
Релейный элемент осуществляет квантование непрерывного сигнала Х по уровню, преобразуя его в дискретный сигнал У. Релейный элемент – это звено релейного действия, статическая характеристика которого может иметь вид, показанный на рис. 3.38.
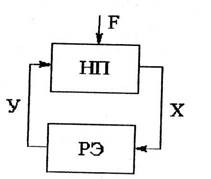
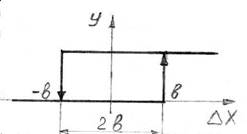
Рис.3.37. Релейные АСР Рис.3.38. Статическая характеристика
двухпозиционного регулятора
Простейшей релейной АСР является, например, система регулирования температуры в сушильном шкафу (рис.3.39).
Для измерения температуры здесь используется термометр ртутный контактный ТРК. После включения рубильника температура в сушильном шкафу (СШ) повышается, достигает заданной, контакты термометра ТРК замкнутся ртутным столбиком и катушка электромагнитного реле ЭР окажутся под напряжением и в результате разомкнется контакт Кэр и электронагревательный элемент ЭН обесточится. В результате будет понижаться температура, контакты термометра ТРК разомкнутся, катушка реле ЭР обесточится, контакт Кэр замкнется и вновь начнется нагрев.
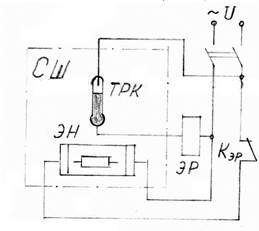
Рис.3.39. АСР температуры в сушильном шкафу
По типу релейных элементов релейные АСР называются двухпозиционными, трехпозиционными и т.д. Многопозиционное квантование по уровню применяется главным образом в цифровых САУ.
Простота релейных схем объясняется тем, что устройства релейного действия, как правило, значительно проще непрерывного пропорционального действия.
Релейные АСР получили широкое распространение благодаря своей простоте, однако имеют и существенные недостатки: регулируемая величина совершает незатухающие колебания около заданного значения даже при отсутствии внешних возмущающих воздействий (режим автоколебаний).
3.10.3. Автоколебания в релейных АСР
Из релейных АСР наибольшее распространение в промышленности получили системы двухпозиционного регулирования (СДР). Как следует из примера СДР температуры (рис.3.39), электронагреватель сушильного шкафа может быть либо включенным, либо выключенным, а температура в его рабочем пространстве может либо возрастать, либо уменьшаться относительно заданного значения.
Этот режим работы релейных систем регулирования называется автоколебательным, а возникшие незатухающие колебания регулируемой величины – автоколебаниями (автономными колебаниями).
Качество переходного процесса при регулировании в таких системах определяется параметрами автоколебаний – амплитудой и частотой (или периодом). Анализ автоколебаний в СДР ведется на основе ее структурной схемы, представляющей последовательное соединение релейного элемента РЭ и линейной части с передаточной функцией Wл.ч(Р) (рис.3.40). При этом линейная часть системы состоит из всех элементов АСР, за исключением релейного, т.е. из объекта регулирования, измерительного устройства, различных внутренних связей и др.

Рис.3.40. Структурная схема релейной АСР с запаздыванием.
Одновременно в структурной схеме имеется обратная связь через звено чистого запаздывания e-pτ, где время запаздывания τ равно сумме запаздываний объекта регулирования τоб и датчика τд.
В схеме на рис.3.40 введены относительные величины. Относительное значение регулируемой величины представлено
| φ2 = | x2 -хНАЧ | = | x2 -хНАЧ | , (3.49) |
| хКОН - хНАЧ | А |
где хнач - установившееся значение регулируемой величины, соответствующее минимальной позиции регулируемого воздействия (команды управления); хкон – установившееся значение регулируемой величины, соответствующее максимальной позиции регулирующего воздействия (команды управления); А = хкон - хнач - зона регулирования.
Зона неоднозначности в относительных координатах 2σ = 2b/А, задаваемое значение регулируемой величины φ1 = (х1-хнач)/А.
Очевидно, 0<φ2<1, т.к. из (3.49) следует, что при х2→ хнач φ2 →0, а при х2→хкон φ2→1.
Следовательно, зона регулирования в этом случае Аφ = 1 -0=1.
Регулятор получает информацию об изменении регулируемой величины с запаздыванием τ и размах автоколебаний равен уже не 2σ (в относительных единицах), а больше (рис. 3.41). приращения Δσ1 и Δσ2 возникают благодаря тому, что вследствие инерционности объекта переключение регулирующего воздействия происходит на время τ позже.
Штриховая кривая на рис. 3.41 соответствует изменению
φ 2*(t) = φ 2 (t-τ).

Рис.3.41.Определение параметров автоколебаний
в релейной двухпозиционной АСР с запаздыванием.
Для определения параметров автоколебаний проведем секущие через точки А, В и С, Д до пересечения с линиями установившихся значений φ2 =1 и φ2 =0. В результате геометрических построений образуется две пары подобных треугольников: Δ ΑGF ~ Δ ΑΒΕ и Δ CNM ~ Δ CDH. Следовательно, АЕ/ВЕ=АF/FG и СН/НD = СМ/МN, откуда АЕ=ВЕ·AF/FG и CH=HD·CM/MN.
Учитывая, что АЕ = Δσ1; ВЕ = τ ; А F = 1-φ1 -σ; FD=Т + τ/2; СН=Δσ2; НD=τ; СМ = φ1 –σ; МN=Т+ τ/2, получим
| Δσ1 = | τ | ∙ (1-φ1 –σ ) | } | (3.50) |
| Т+ τ/2 | ||||
| Δσ2 = | τ | ∙ ( φ1 –σ ) | ||
| Т+ τ/2 |
Тогда размах автоколебаний в относительных величинах будет:
| 2 σ* = 2 σ + Δσ1 + Δσ2 =2 σ + | τ | ∙( 1- 2 σ) | . (3.51) |
| Т+ τ/2 |
В абсолютных величинах размах автоколебаний будет равен 2σ*А.
Период автоколебаний можно определить по формуле
ТА = 2σ*Тξ , (3.52)
| где | ξ = | (3.53) | |
| φ1∙(1-φ1) |
Подставив 2σ = 2σ* , получаем ТА = 2σ*Тξ . (3.54)
Приращения амплитуды колебаний Δσ1 и Δσ2 зависят от отношения τ/Т. Для больших значений этого отношения релейные АСР могут оказаться непригодными. Практика показывает,что для удовлетворительной работы релейной АСР необходимо , чтобы τ /Т≤0,2.
Дата добавления: 2021-02-19; просмотров: 901;











