Назначение и особенности спектрального анализа нестационарных дискретных сигналов. Понятие о частотно-временных преобразованиях.

С позиций анализа произвольных сигналов и функций в частотной области и точного их восстановления после преобразований можно отметить ряд недостатков разложения сигналов в ряды Фурье:

- ограниченная информативность анализа нестационарных сигналов и отсутствие возможностей анализа их особенностей, т.к. в частотной области происходит «размазывание» особенностей сигналов (разрывов, ступенек, пиков) по всему частотному диапазону спектра;

- гармонические базисные функции разложения не способны отображать перепады сигналов с бесконечной крутизной типа прямоугольных импульсов, т.к. для этого требуется бесконечно большое число членов ряда. При ограничении числа членов ряда Фурье в окрестностях скачков и разрывов при восстановлении сигнала возникают осцилляции (явление Гиббса);

- преобразование Фурье отображает глобальные сведения о частотах исследуемого сигнала и не дает представления о локальных свойствах сигнала при быстрых временных изменениях его спектрального состава. Преобразование Фурье не различает стационарный сигнал с суммой двух синусоид от нестационарного сигнала с двумя последовательно следующими синусоидами с теми же частотами.

В ряде практически важных случаев: анализ речи, сейсмических колебаний и других, анализируемый сигнал является принципиально нестационарным и имеет спектр, параметры которого меняются во времени. В этом случае классическое спектральное оценивание является непригодным и используют частотно-временные преобразования.

Под частотно-временным преобразованием понимается некоторая совместная функция времени и частоты, характеризующая распределение спектра в частотно-временной плоскости.

Простейшим примером является частотно-временного преобразования дееется текущее преобразование Фурье:

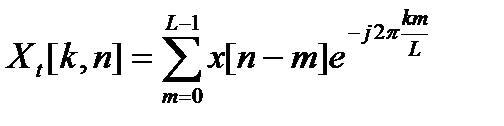, (12.1)

где 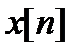– дискретные отсчеты сигнала;

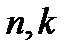– индексы дискретных отсчетов по времени и частоте соответственно;

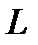– длина дискретного преобразования Фурье.

Результат 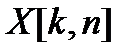вычисляется в координатах частота – время и представляет собой ДПФ, вычисляемое для каждого из моментов времени с учетом использования прямоугольного весового окна. Текущее преобразование Фурье можно дополнить, умножив сигнал на весовое окно :

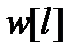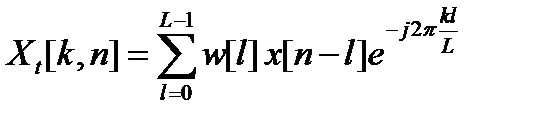. (12.2)