Кореллограммная оценка спектральной плотности мощности дискретного случайного процесса.

По теореме Винера-Хинчина корреляционная функция и спектральная плотность мощности (СПМ) дискретного случайного процесса связаны преобразованием Фурье:

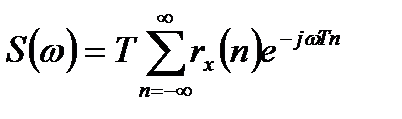. (11.21)

где T – интервал дискретизации сигнала;

.

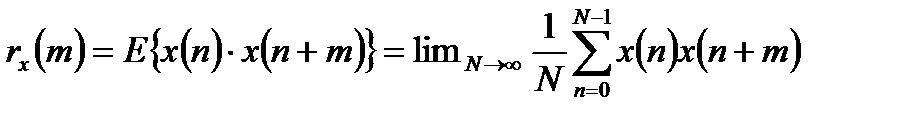Коррелограммный метод оценивания СПМ заключается в подстановке в последнее выражение (11.21) 1) конечной суммы 2) значений оценки автокорреляции вместо бесконечной последовательности неизвестных истинных значений автокорреляции.

На практике имеется ограниченная последовательность отсчетов x[n], n=0,…,N-1 и в качестве оценки корреляционной функции принимается следующая функция

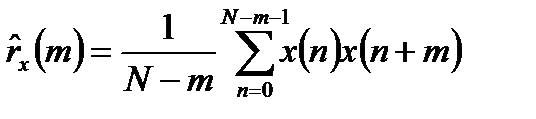. (11.22)

Это оценка называется несмещенной, так как ее математическое ожидание равно истинной автокорреляционной оценке:

.

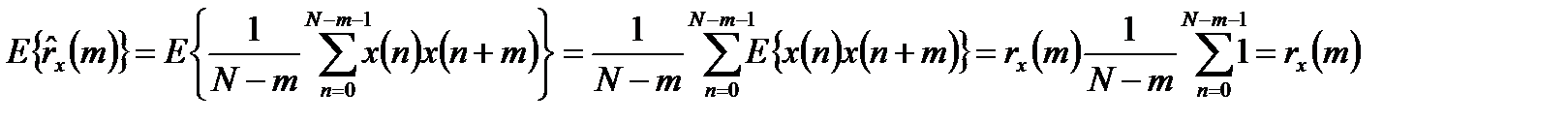Кроме того, на практике часто используют смещенную оценку корреляционной функции:

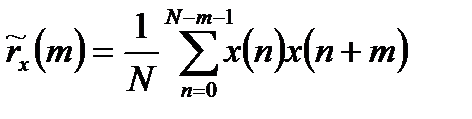. (11.23)

Эта оценка называется смещенной, так как ее математическое ожидание будет равно взвешенной истинной автокорреляционной оценки:

.

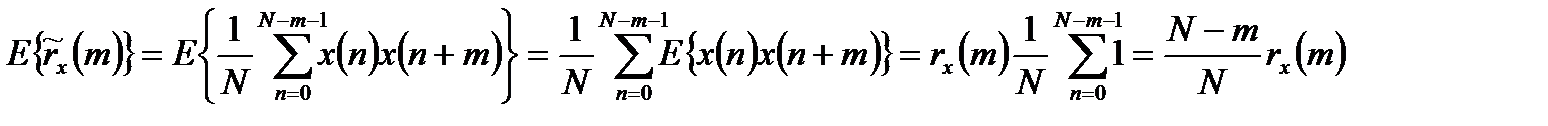После получения оценки корреляционной функции для вычисления СПМ применяется весовая функция:

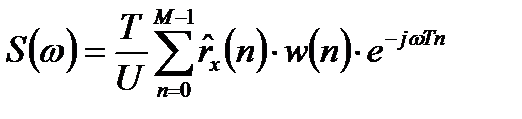, (11.24)

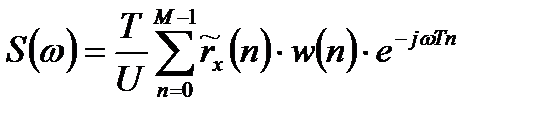, (11.25)

где .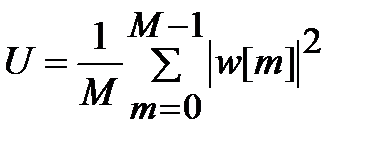

Кривошеев В.И. Современные методы цифровой обработки сигналов (цифровой спектральный анализ). Учебно-методические материалы / В.И. Кривошеев. – Нижний Новгород, 2006. – 117 с.

Романюк Ю.А. Дискретное преобразование Фурье в цифровом спектральном анализе. Учебное пособие. – М.: МФТИ, 2007. – 120 с.