Дискретные автоматические системы

Управления

В автоматических системах управления применяются два основных способа пере-дачи и преобразования сигналов – непрерывный и дискретный. При непрерывном способе передаётся и преобразуется каждое мгновенное значение сигнала, а при дискретном – сигнал, квантованный по времени или уровню.

Различают три вида квантования сигналов – по времени, по уровню и одновре-менно по времени и уровню. Автоматические системы управления в которых имеет место процесс квантования сигналов по времени, называются импульсными. Сис-темами, в которых осуществляется квантование по уровню, являются релейные (позиционные) автоматические системы управления. Системы, в которых проис-ходит процесс квантования сигналов по времени и уровню, называются цифровы-ми автоматическими системами управления.

Работа дискретных систем связана с передачей и преобразованием последова-тельности импульсов. Разработка методов расчёта дискретных систем регулирова-ния связана в первую очередь с применением цифровых вычислительных ус-тройств в контуре управления. Информация, обрабатываемая в цифровых вычисли-тельных устройствах, представляет комбинации электрических импульсов, или, так называемые, кодовые комбинации. При использовании цифровой вычислительной машины в качестве регулятора необходимо предусмотреть в составе системы регу-лирования устройства, преобразующие непрерывные сигналы в кодовые комби-нации для ввода в ЦВМ, а также устройства, преобразующие коды в непрерывные сигналы для вывода управляющих воздействий из ЦВМ. Таким образом, структура дискретной системы – это сочетание аналоговой части и импульсного элемента.

Импульсный элемент представляет собой модулятор импульсов, преобразующий непрерывно изменяющийся входной сигнал x(t) в последовательность модулиро-ванных импульсов y(t). Различные виды модуляции приведены на рис. 35. При амплитудно-импульсной модуляции АИМ непрерывный сигнал преобразуется в последовательность импульсов постоянной длительности 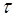и периода следования T, амплитуда которых пропорциональна амплитуде непрерывного сигнала.

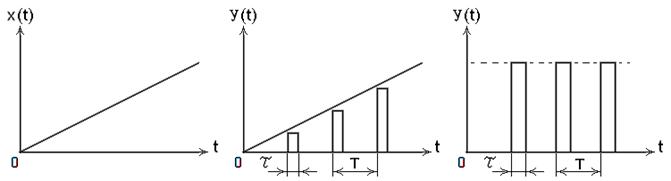
Рис. 35. Входной и выходной сигналы импульсных элементов различных типов:

а. – входной сигнал; б. – выходной сигнал импульсного элемента с АИМ;

в. – выходной сигнал импульсного элемента с ШИМ.

При широтно-импульсной модуляции ШИМ непрерывный входной сигнал пре-образуется в последовательность импульсов постоянной амплитуды и периода сле-дования, длительность которых пропорциональна величине входного сигнала.

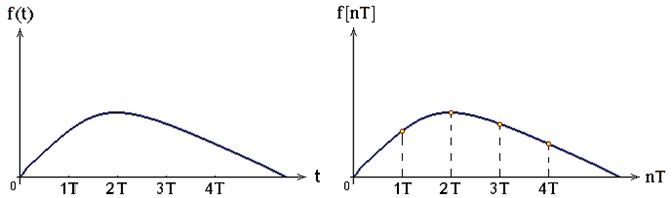
Наличие в структуре дискретной системы импульсного элемента приводит к то-му, что любая дискретная система реагирует на внешнее непрерывное воздействие лишб в дискретные равноотстоящие друг от друга моменты времени. При анализе дискретных систем непрерывную функцию времени f(t) заменяют решётчатой функцией f [nT], значения которой изменяются при дискретных равноотстоящих значениях независимо переменной t. Между этими значениями решётчатая фун-кция равна нулю (рис. 36).

а. б.

Рис. 36. Виды функций:

а – непрерывная; б – решётчатая.

Подобно тому, как скорость изменения непрерывной функции характеризуется первой производной df/dt, скорость изменения решётчатой функции характеризу-ется её первой разностью

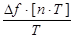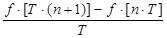= . (2.141)

Умножив левую и правую части на Т, получим

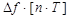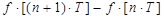= . (2.142)

Аналогично вторая разность

= - = - -

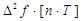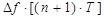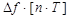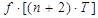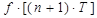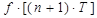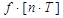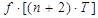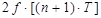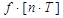- + = - + .(2.143)

Если работа непрерывных систем описывалась обыкновенными дифференциаль-ными уравнениями, содержащими функцию и её производные, то работа дискрет-ных систем описывается уравнением в конечных разностях, или разностным урав-нением, которое содержит решётчатую функцию и её разности.

Апериодическое звено 1-го порядка в непрерывных системах описывается диф-ференциальным уравнением вида

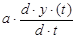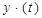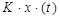_{+ =} .(2.144)

В дискретных системах это звено описывается разностным уравнением вида

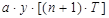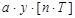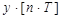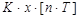_{- + = .} (2.145)

Методы решения разностных и дифференциальных уравнений аналогичны. Для решения обыкновенных дифференциальных уравнений при расчёте непрерывных систем широко применяется операторный метод, основанный на преобразованиях Лапласа. Для решения разностных уравнений применяют аналогичный метод,

основанный на дискретных преобразованиях Лапласа.