Связь спектра дискретизированного сигнала со спектром исходного сигнала. Теорема Котельникова.
2.3.1. Связь спектра дискретизированного сигнала со спектром исходного сигнала
Найдем связь между спектром дискретизированного сигнала 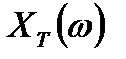 и спектром исходного сигнала
и спектром исходного сигнала 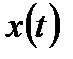 до его дискретизации. Для этого учтем выражение для обратного преобразования Фурье:
до его дискретизации. Для этого учтем выражение для обратного преобразования Фурье:
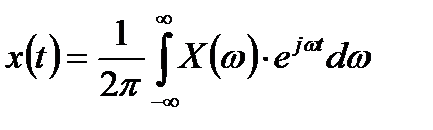 .
.
Соответственно, можно записать следующую связь со спектром исходного непрерывного сигнала 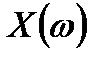 :
:
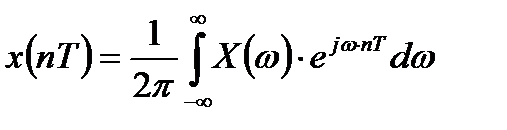 .
.
Подставим это соотношение в выражение для спектра дискретизированного сигнала:
 .
.
Учтем, что
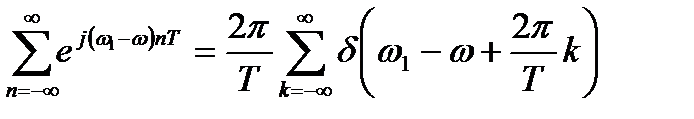 .
.
Воспользуемся фильтрующим свойством дельта-функции:
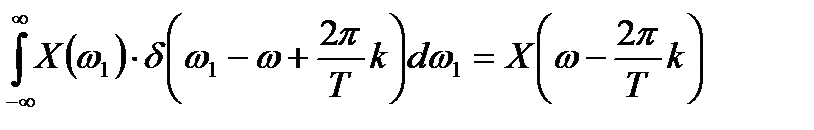 .
.
Результирующая связь спектра дискретизированного сигнала со спектром исходного непрерывного сигнала описывается выражением:
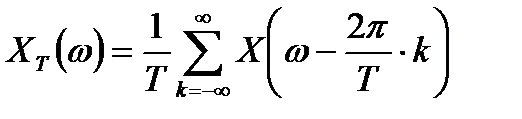 . (2.13)
. (2.13)
Таким образом, спектр дискретизированного сигнала представляет собой периодическую последовательность на оси частот спектров исходного непрерывного сигнала с интервалом частоты дискретизации 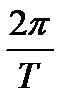 .
.
2.2.3.2. Восстановление исходного непрерывного сигнала. Теорема Котельникова.
Если верхняя граничная частота исходного непрерывного сигнала 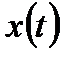 ограничена условием
ограничена условием
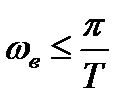 , (2.14)
, (2.14)
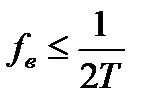
то отдельные копии спектра 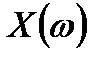 не накладываются друг на друга в спектре дискретизированного сигнала.
не накладываются друг на друга в спектре дискретизированного сигнала.
Рисунок 2.2 – восстановление исходного непрерывного сигнала
В этом случае ( 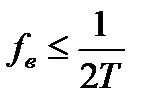 ) исходный непрерывный сигнал
) исходный непрерывный сигнал 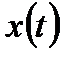 может быть полностью восстановлен с помощью идеального ФНЧ, имеющего прямоугольную ЧХ:
может быть полностью восстановлен с помощью идеального ФНЧ, имеющего прямоугольную ЧХ:
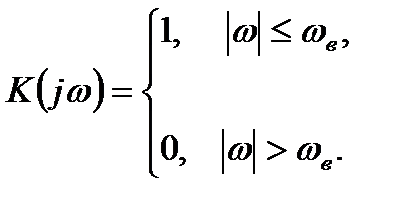
Импульсная характеристика такого фильтра является обратным преобразованием Фурье от частотной характеристики:
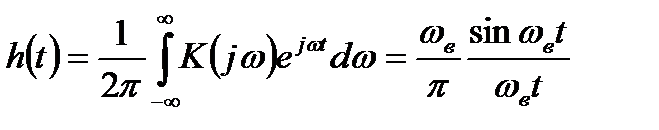 .
.
В соответствии с интегралом Дюамеля можно восстановить исходный ограниченный по спектру сигнал следующим образом:
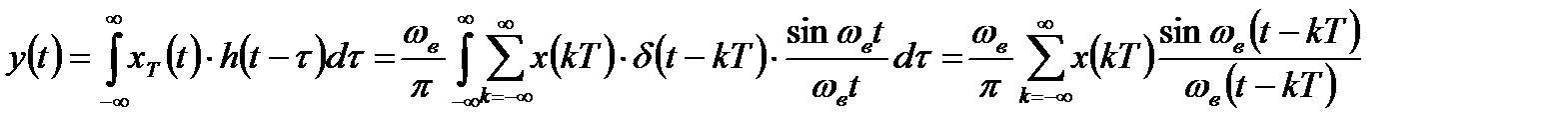 . (2.15)
. (2.15)
Точная формулировка теоремы Котельникова имеет следующий вид:
Произвольный сигнал, спектр которого не содержит частот выше  , может быть полностью восстановлен, если известны дискретные значения этого сигнала, взятые через равные промежутки времени
, может быть полностью восстановлен, если известны дискретные значения этого сигнала, взятые через равные промежутки времени 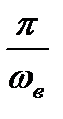 .
.
Дата добавления: 2020-08-31; просмотров: 836;











