Свойства дискретного преобразования Фурье

1. Линейность ДПФ. ДПФ суммы дискретных последовательностей длительности N равно сумме ДПФ слагаемых суммы и имеет длину N:

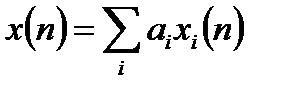; (3.6)

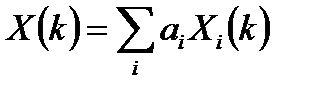. (3.7)

2. ДПФ сумм последовательностей разной длины. Если в исходной сумме последовательностей 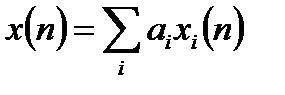разные длины: N₁, N₂, N₃, …, то перед вычислением ДПФ всей последовательности необходимо привести последовательности к одинаковой длине N, равной максимальной длине исходных последовательностей, за счет дополнения нулями.

3. Сдвиг ДПФ. Сдвиг ДПФ по оси k вправо на величину k₀ соответствует умножению исходной последовательности на комплексную экспоненту:

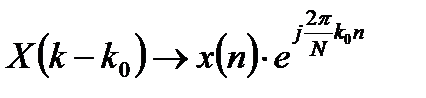. (3.8)

4. Сдвиг исходной последовательности. Сдвиг последовательности вправо на m отсчетов (задержка последовательности) соответствует умножению ДПФ на комплексную экспоненту:

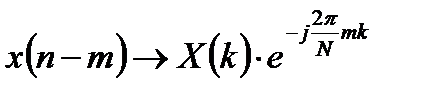. (3.9)

5. Теорема Парсеваля.

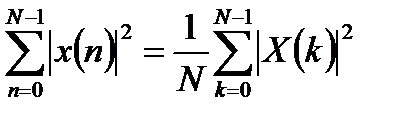. (3.10)

Теорема Парсеваля утверждает, что энергию сигнала можно вычислить как во временной, так и в частотной области.

6. Свойство симметрии. Свойство симметрии вещественной последовательности:

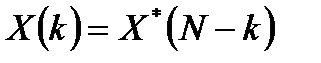, (3.11)

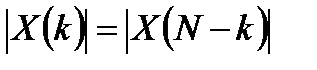, (3.12)

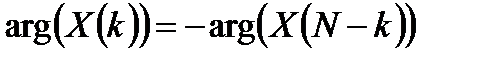; (3.13)

ось симметрии проходит через точку .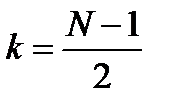

Для четного N:

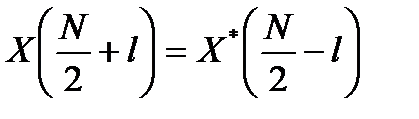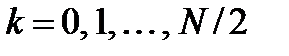, . (3.14)

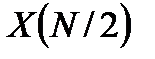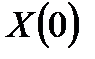Из последнего равенства следует, что и всегда действительные числа.

7. ДПФ вещественной последовательности. ДПФ вещественной последовательности полностью определено на интервале 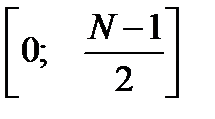, который соответствует основному спектру сигнала.

Литература

Романюк Ю.А. Дискретное преобразование Фурье в цифровом спектральном анализе. Учебное пособие. – М.: МФТИ, 2007. – 120 с.