Преобразование Фурье дискретизированного сигнала
2.2.1. Ряд Фурье для непрерывных периодических сигналов
Непрерывная периодическая функция времени 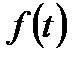 с периодом
с периодом 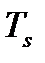 может быть представлена рядом Фурье:
может быть представлена рядом Фурье:
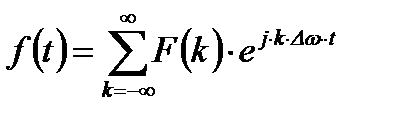 , (2.5)
, (2.5)
где 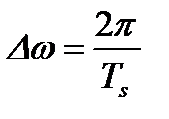 - период дискретизации по частоте
- период дискретизации по частоте 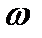 ;
;
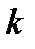 - нормированная частота;
- нормированная частота;
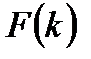 - коэффициенты Фурье в виде комплексных чисел.
- коэффициенты Фурье в виде комплексных чисел.
Коэффициенты Фурье 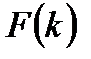 вычисляются по формуле:
вычисляются по формуле:
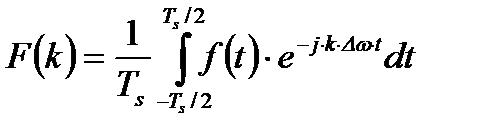 . (2.6)
. (2.6)
В свою очередь, можно ввести следующую непрерывную периодическую функцию частоты 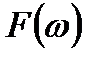 с периодом
с периодом 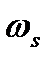 , которая может быть представлена следующим рядом Фурье:
, которая может быть представлена следующим рядом Фурье:
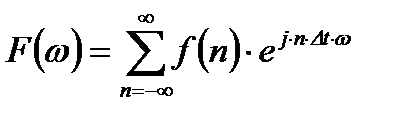 , (2.7)
, (2.7)
где 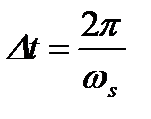 - период дискретизации по времени
- период дискретизации по времени 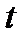 ;
;
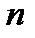 - нормированное время, соответствующее абсолютному времени
- нормированное время, соответствующее абсолютному времени 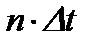 ;
;
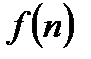 - коэффициенты Фурье в виде комплексных чисел.
- коэффициенты Фурье в виде комплексных чисел.
Коэффициенты Фурье 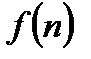 вычисляются по формуле:
вычисляются по формуле:
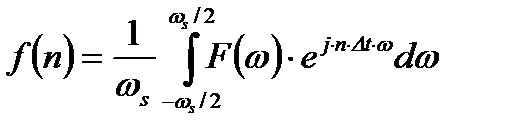 . (2.8)
. (2.8)
2.2.2. Преобразование Фурье для непрерывных непериодических сигналов
В результате предельного перехода при 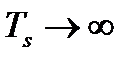 можно перейти от ряда Фурье (2.5)
можно перейти от ряда Фурье (2.5)
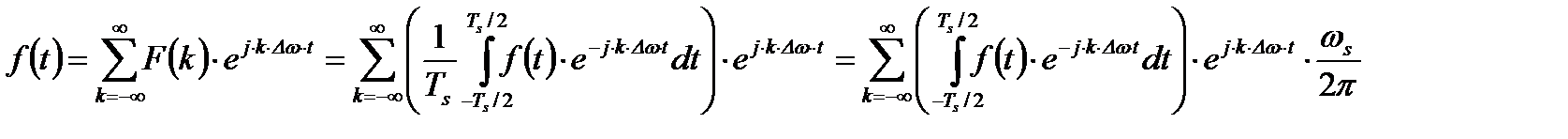
к интегралу Фурье:
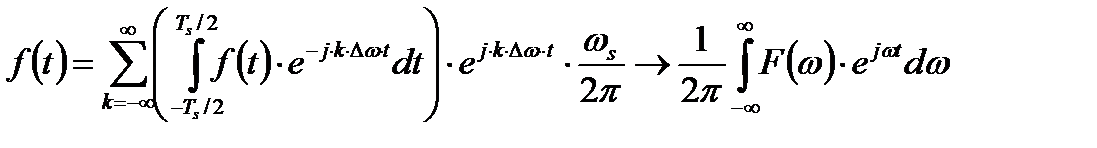 , (2.9)
, (2.9)
где 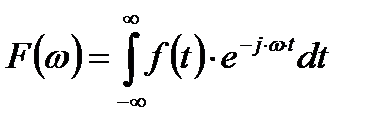 - спектральная плотность функции
- спектральная плотность функции 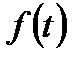 . (2.10)
. (2.10)
2.2.3. Преобразование Фурье дискретизированного сигнала
Преобразование Фурье дискретизированного сигнала запишется в виде:
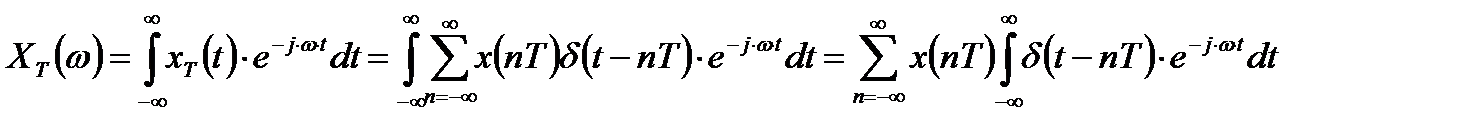 .
.
Воспользовавшись фильтрующим свойством дельта – функции, получим:
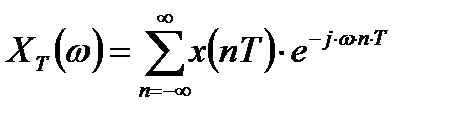 . (2.11)
. (2.11)
Спектр дискретизированного сигнала 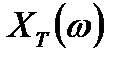 характеризуется двумя свойствами:
характеризуется двумя свойствами:
1) является непрерывной функцией частоты;
2) является периодической функцией частоты.
Соотношение (2.11) является одновременно:
- прямым преобразованием Фурье дискретизированного сигнала 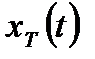 ;
;
- рядом Фурье непрерывной функции 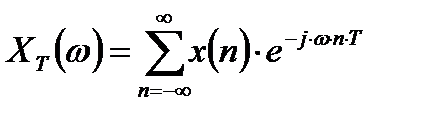 .
.
Поэтому коэффициенты 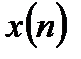 ряда Фурье могут быть вычислены по известной формуле для коэффициентов ряда Фурье (2.6):
ряда Фурье могут быть вычислены по известной формуле для коэффициентов ряда Фурье (2.6):
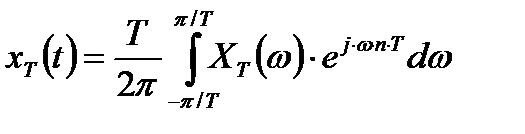 . (2.12)
. (2.12)
Соотношение (2.12) является одновременно:
- обратным преобразованием Фурье для дискретного сигнала 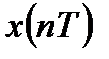 ;
;
- коэффициентом ряда Фурье непрерывной функции 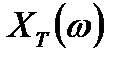 .
.
Таким образом, преобразованием Фурье дискретизированного сигнала 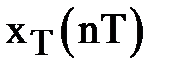 называется пара взаимно однозначных преобразований:
называется пара взаимно однозначных преобразований:
прямое преобразование 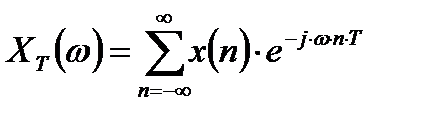 ;
;
и обратное преобразование 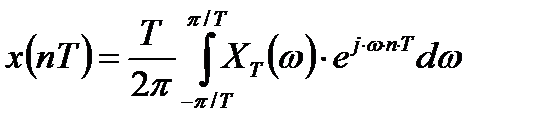 .
.
Дата добавления: 2020-08-31; просмотров: 796;











