ДИФФУЗИОННЫЕ ХАРАКТЕРИСТИКИ ВЕЩЕСТВА И ИХ РАСЧЕТ
Полученное в диффузионном приближении выражение для длины диффузии справедливо лишь в случае слабого поглощения.
Отказавшись от рассмотрения уравнения переноса тепловых нейтронов в диффузионном приближении, можно показать, что в общем случае длина диффузии определяется трансцендентным уравнением (приводим без вывода)
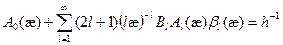 , (8.185)
, (8.185)
где 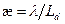 ;
; 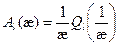 [
[ 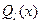 — функция Лежандра II рода порядка l].
— функция Лежандра II рода порядка l].
Величины 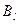 представляют собой коэффициенты разложения индикатрисы рассеяния по полиномам Лежандра относительно косинуса угла рассеяния. Функции
представляют собой коэффициенты разложения индикатрисы рассеяния по полиномам Лежандра относительно косинуса угла рассеяния. Функции 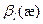 удовлетворяют рекуррентному соотношению:
удовлетворяют рекуррентному соотношению:
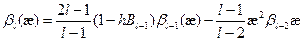 , (8.186)
, (8.186)
причем
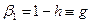 ;
; 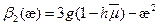 .
.
Величина 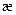 зависит от полной вероятности рассеяния h и типа индикатрисы рассеяния, определяемого набором коэффициентов ее разложения {
зависит от полной вероятности рассеяния h и типа индикатрисы рассеяния, определяемого набором коэффициентов ее разложения { 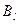 }. Следовательно, имеется возможность приближенного определения типа индикатрисы рассеяния на основании диффузионных измерений в замедлителях известного состава.
}. Следовательно, имеется возможность приближенного определения типа индикатрисы рассеяния на основании диффузионных измерений в замедлителях известного состава.
На рис. 40 представлены результаты измерений длины диффузии более чем в тридцати различных замедлителях, обработанные в координатах 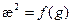 , и зависимости, вычисленные по уравнению (98) для изотропной и линейно-анизотропной индикатрис рассеяния (для последней — при двух значениях среднего косинуса угла рассеяния
, и зависимости, вычисленные по уравнению (98) для изотропной и линейно-анизотропной индикатрис рассеяния (для последней — при двух значениях среднего косинуса угла рассеяния 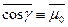 ). Экспериментально полученные зависимости дифференцированы по типам индикатрис рассеяния, причем это особенно заметно в случае «отравленных» сред (
). Экспериментально полученные зависимости дифференцированы по типам индикатрис рассеяния, причем это особенно заметно в случае «отравленных» сред ( 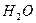 и
и 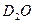 ). Важно отметить, что для интерпретации всего многообразия данных оказывается достаточным представление об анизотропии рассеяния первого порядка. Усиление анизотропии рассеяния в водных растворах поглотителя при увеличении концентрации последнего, объясняется ужестчением спектра тепловых нейтронов (повышением температуры нейтронного газа).
). Важно отметить, что для интерпретации всего многообразия данных оказывается достаточным представление об анизотропии рассеяния первого порядка. Усиление анизотропии рассеяния в водных растворах поглотителя при увеличении концентрации последнего, объясняется ужестчением спектра тепловых нейтронов (повышением температуры нейтронного газа).
Зависимость 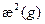 есть по существу зависимость обратного квадрата длины диффузии тепловых нейтронов от числа рассеивающих столкновений n до поглощения в среде (совпадающего с обратной величиной вероятности поглощения g-1). Физически этот результат следует из того, что число
есть по существу зависимость обратного квадрата длины диффузии тепловых нейтронов от числа рассеивающих столкновений n до поглощения в среде (совпадающего с обратной величиной вероятности поглощения g-1). Физически этот результат следует из того, что число 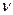 столкновений до поглощения равно отношению длины пути
столкновений до поглощения равно отношению длины пути 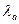 , проходимого нейтроном до поглощения, к полной длине свободного пробега
, проходимого нейтроном до поглощения, к полной длине свободного пробега 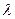 :
:
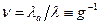 .
.
При слабом поглощении (g<<1) уравнение (98) дает явное выражение для 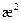
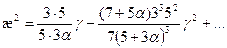 , (8.188)
, (8.188)
где
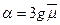 ;
; 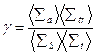 .
.
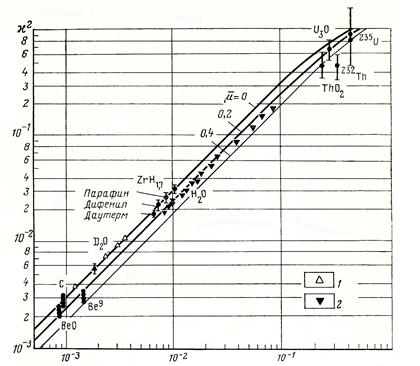
Число столкновений
Рис.8.24. Универсальная зависимость для определения обратного квадрата длины диффузии тепловых нейтронов в единицах 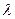 (по Д.А.Кожевникову).
(по Д.А.Кожевникову).
1 — 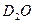 (отравление бором); 2 —
(отравление бором); 2 — 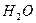 (отравление бором и кадмием). Экспериментальные данные различных исследователей: по
(отравление бором и кадмием). Экспериментальные данные различных исследователей: по 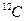 — А. В. Антонов и др. (ФИАН); Ч. Титтл,. Э. Сегре, Л., Карлбом, И. Саго и Г. Теллье; по ВеО — И. Ф. Жежерун (ИАЭ), А. Кехлин; по Be— А. К. Красин и др., И. Ф. Жежерун (ИАЭ), данные КАЭ США; по
— А. В. Антонов и др. (ФИАН); Ч. Титтл,. Э. Сегре, Л., Карлбом, И. Саго и Г. Теллье; по ВеО — И. Ф. Жежерун (ИАЭ), А. Кехлин; по Be— А. К. Красин и др., И. Ф. Жежерун (ИАЭ), данные КАЭ США; по 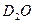 — С. Кэш и-Д. Вудс; В. Раевский, Н. Бауманн, Н. Гангули и др.; по даутерму — М. Кюхле, Л. Н. Юрова и др.(МИФИ), Ф. Деманинс; по дифенилу — Л. ,Н. Юрова и др., Р. Бауэр, А. Бод и др.; по парафину — Ч. Титтл, Б. Гримланд, Л. Эш; по гидриду циркония — Дж. Мидоус; по
— С. Кэш и-Д. Вудс; В. Раевский, Н. Бауманн, Н. Гангули и др.; по даутерму — М. Кюхле, Л. Н. Юрова и др.(МИФИ), Ф. Деманинс; по дифенилу — Л. ,Н. Юрова и др., Р. Бауэр, А. Бод и др.; по парафину — Ч. Титтл, Б. Гримланд, Л. Эш; по гидриду циркония — Дж. Мидоус; по 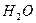 — А. В. Антонов и др.; М. Рейер, Н. Матееску и В. Нагорняк, Дж. де Юрен и Г. Розенвассер; Н. Шостранд, Г. фон Дардел; по
— А. В. Антонов и др.; М. Рейер, Н. Матееску и В. Нагорняк, Дж. де Юрен и Г. Розенвассер; Н. Шостранд, Г. фон Дардел; по 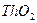 ,
, 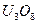 , Th и
, Th и 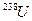 — данные комиссии по атомной энергии США.
— данные комиссии по атомной энергии США.
Если выполняется (при слабом поглощении) условие 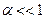
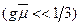 , то (8.188) приобретает вид
, то (8.188) приобретает вид
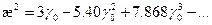 , (8.188
, (8.188  )
)
где
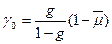 .
.
Диффузионному приближению, справедливому при слабом поглощении, соответствует первый член в разложении (8.188'). На рис. 41 показана зависимость обратного квадрата длины диффузии от величины полного макроскопического сечения поглощения водного раствора поглотителя (в единицах макроскопического сечения поглощения тепловых нейтронов протонами), построенная по экспериментальным данным различных исследователей в сравнении с предсказанием теории диффузии. Этот график служит конкретной иллюстрацией области применимости диффузионного приближения в поглощающих средах.
При больших поглощениях уравнение диффузии и уравнение переноса дают качественно различные результаты. Согласно диффузионному приближению 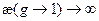 , тогда как из теории переноса и очевидных физических соображений необходимо, чтобы
, тогда как из теории переноса и очевидных физических соображений необходимо, чтобы 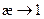 (при
(при 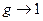 число взаимодействий тепловых нейтронов ν→1). Интересное обстоятельство, выявленное при численном расчете, состоит в том, что минимальная величина длины диффузии, равная величине полного свободного пробега, достигается не асимптотически, а выходит на насыщение при некотором конечном сечении поглощения.
число взаимодействий тепловых нейтронов ν→1). Интересное обстоятельство, выявленное при численном расчете, состоит в том, что минимальная величина длины диффузии, равная величине полного свободного пробега, достигается не асимптотически, а выходит на насыщение при некотором конечном сечении поглощения.

Рис.8.25. Зависимость обратного квадрата длины диффузии от величины полного макроскопического сечения поглощения водного раствора поглотителя. 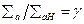 . Результаты экспериментов по методу «отравления» (М. Рейер, М. Матеску, В. Нагорняк)
. Результаты экспериментов по методу «отравления» (М. Рейер, М. Матеску, В. Нагорняк)
Рассмотрим температурную зависимость длины диффузии и коэффициента диффузии тепловых нейтронов. После открытия явления замедления нейтронов оставалось неясным, достигают замедленные нейтроны тепловых скоростей, или нет. П. И. Лукирский и Т. В. Царева (1935 г.) впервые убедительно показали, что в спектре замедленных нейтронов существует область, зависящая от термодинамической температуры замедлителя. Таким образом, было установлено, что замедленные нейтроны действительно приходят в тепловое равновесие с веществом замедлителя. Зависимость длины диффузии тепловых нейтронов от температуры была обнаружена Э. Ферми и грубо измерена для воды уже в 1942 г.
Температурные зависимости диффузионных параметров измерены для целого ряда замедлителей. Наибольшее число экспериментов выполнено с обычной водой (рис. 42).
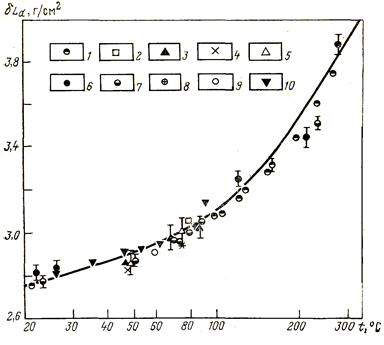
Рис.8.26. Расчетная зависимость (кривая) массовой длины диффузии dLd тепловых нейтронов в воде от температуры (по Д.А.Кожевникову).
Экспериментальные данные: 1- А. В. Антонов и др. (1962 г.); 2- А. В. Антонов и др. (1955 г.); 3 - И. Чикаи и др.; 4- В. Дно; 5 - В. Дио, Е. Шоппер; 6 - М. Кюхле; 7- В. Лопец, Л. Байстер; 8 - М. Рейер, Дж. де Юрен; 9 - К. Рокей, В. Сколник; 10 - В. Уилсон и др.
Изменение диффузионных параметров тепловых нейтронов с повышением температуры замедлителя объясняется ужестчением спектра тепловых нейтронов и изменением плотности вещества. Повышение скорости нейтронов вызывает увеличение коэффициента диффузии и, вследствие уменьшения сечения захвата, — длины диффузии.
Изменение диффузионных параметров с температурой наиболее существенно влияет на пространственное распределение тепловых нейтронов в средах со слабым поглощением, когда длина диффузии больше длины замедления или сравнима с ней по величине.
Рассмотрим количественную связь диффузионных характеристик замедлителя с его температурой при слабом поглощении, когда
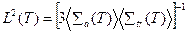 .
.
Примем, что сечение переноса тепловых нейтронов изменяется с энергией по закону
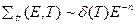 , n>0
, n>0
а сечение захвата — по закону 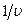 :
:
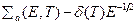 .
.
Тогда [36]
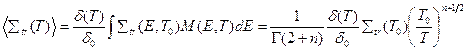
(интегрирование распространено до бесконечности, поскольку подынтегральная функция быстро убывает при 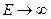 );
); 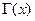 — гамма-функция Эйлера.
— гамма-функция Эйлера.
Зависимость длины диффузии от температуры приобретает следующий вид:
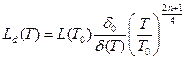 , (8.189)
, (8.189)
где
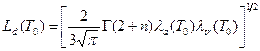 .
.
При относительно слабом поглощении коэффициент диффузии тепловых нейтронов определяется выражением
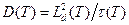
(при сильном поглощении эта величина, в отличие от длины диффузии, теряет физический смысл).
При поглощении по закону 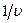 произведение
произведение 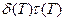 не зависит от температуры. Температурная зависимость величины
не зависит от температуры. Температурная зависимость величины 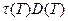 совпадает с температурной зависимостью квадрата длины диффузии:
совпадает с температурной зависимостью квадрата длины диффузии:
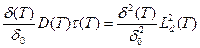 ,
,
и, следовательно
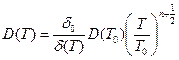 , (8.190)
, (8.190)
где
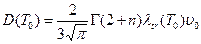 ,
,
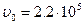
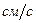
Отсюда следует, что по результатам измерений температурных зависимостей диффузионных характеристик можно установить характер зависимости сечений переноса от энергии нейтронов. Результаты расчетов температурной зависимости длины диффузии нейтронов в воде, выполненных по формуле (8.189) (см. рис.42), хорошо согласуются с экспериментальными данными при n = 0.5, т. е. длина переноса тепловых нейтронов в воде пропорциональна скорости нейтронов.
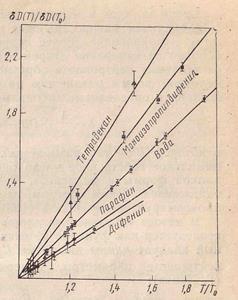
Температурные зависимости диффузионных параметров углеводородов могут быть более сильными (моноизопропилдифенил, тетрадекан) и более слабыми (парафин, дифенил), чем в случае воды, обнаруживая определенную корреляцию с температурной зависимостью вязкости (рис. 43).
Повышение температуры спектра тепловых нейтронов с ростом температуры замедлителя вызывает некоторое уменьшение длины замедления нейтронов до тепловой энергии. Относительное изменение длины замедления 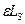 легко может быть оценено:
легко может быть оценено:
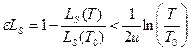 ,
, 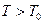 ,
,
(и — летаргия). Поскольку для быстрых нейтронов, замедляющихся до тепловых энергий, 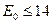 МэВ,
МэВ, 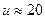 ,
, 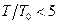 , то
, то 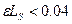 . Изменение пространственного распределения надтепловых нейтронов при высоких температурах и давлениях обусловлено изменением физических свойств замедлителя (плотности).
. Изменение пространственного распределения надтепловых нейтронов при высоких температурах и давлениях обусловлено изменением физических свойств замедлителя (плотности).
Среди методов измерения диффузионных характеристик 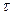 и D наибольшее распространение получили импульсный метод и метод «отравления» (более подробно см. [40, 51, 81]. Первый основан на измерении декремента
и D наибольшее распространение получили импульсный метод и метод «отравления» (более подробно см. [40, 51, 81]. Первый основан на измерении декремента 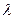 временного спада импульса тепловых нейтронов в образце исследуемого вещества определенной формы различного размера. Измеряемая величина
временного спада импульса тепловых нейтронов в образце исследуемого вещества определенной формы различного размера. Измеряемая величина 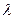 связана с определяемыми параметрами
связана с определяемыми параметрами 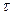 и D уравнением [32]
и D уравнением [32]
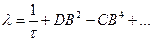 , (8.191)
, (8.191)
в котором 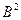 — так называемый «материальный параметр» (минимальное собственное число оператора Лапласа для образца данной формы и размеров), С — коэффициент диффузионного охлаждения. Таким образом, измеряя зависимость
— так называемый «материальный параметр» (минимальное собственное число оператора Лапласа для образца данной формы и размеров), С — коэффициент диффузионного охлаждения. Таким образом, измеряя зависимость 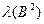 и аппроксимируя ее параболой (8.191), можно определить
и аппроксимируя ее параболой (8.191), можно определить 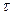 , D и С.
, D и С.
| Таблица 8.1. Показатель n температурных зависимостей диффузионных характеристик для воды и некоторых углеводородных соединений (по Д.А.Кожевникову)
Рис.8.27. Температурная зависимость массового коэффициента диффузии тепловых нейтронов (без плотностного эффекта) для некоторых углеводородных соединений (по экспериментальным данным Л. Н. Юровой и др.) [90] и воды.
|
В методе «отравления» длина диффузии тепловых нейтронов исследуется как функция сечения поглощения вещества. Обратный квадрат длины диффузии 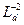 может быть выражен через нейтронные параметры, измеряемые импульсным методом (Г. Хонэк):
может быть выражен через нейтронные параметры, измеряемые импульсным методом (Г. Хонэк):
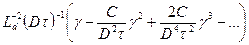 , (8.192)
, (8.192)
где 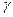 — макроскопическое сечение поглощения, измеренное в единицах макроскопического сечения поглощения «неотравленного» замедлителя. Это соотношение позволяет вычислить длину диффузии не только по параметрам импульсного метода, измеренным в этой же среде, но и по параметрам «неотравленной» среды в «отравленном» замедлителе. В качестве иллюстрации практического применения соотношения (8.192) на рис. 41 сплошной линией показана зависимость
— макроскопическое сечение поглощения, измеренное в единицах макроскопического сечения поглощения «неотравленного» замедлителя. Это соотношение позволяет вычислить длину диффузии не только по параметрам импульсного метода, измеренным в этой же среде, но и по параметрам «неотравленной» среды в «отравленном» замедлителе. В качестве иллюстрации практического применения соотношения (8.192) на рис. 41 сплошной линией показана зависимость 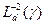 для воды:
для воды:
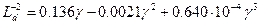 ; (8.192')
; (8.192')
эта зависимость вычислена по данным А. В. Антонова и др. ( 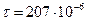 с;
с; 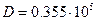
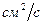 ;
; 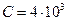
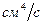 ).
).
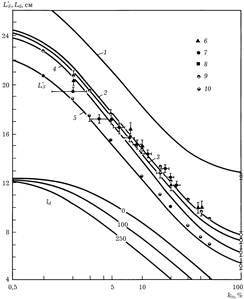
Рис.8.28
Дата добавления: 2020-08-31; просмотров: 828;











