КИНЕТИКА ДИФФУЗИИ НЕЙТРОНОВ

Применив к уравнению (8.156) метод сферических гармоник в 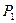- приближении, учтя (77) и выполнив интегрирование по углам и энергиям, получим [36]

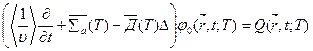(8.160)

Это уравнение совпадает с уравнением диффузии, коэффициенты в котором определяются следующим образом:

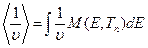; (8.161)

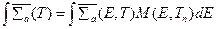; (8.162)

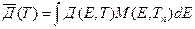; (8.163)

—

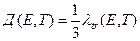коэффициент диффузии для плотности потока; 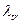— длина переноса или транспортная длина свободного пробега тепловых нейтронов при температуре Т:

.

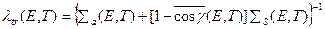Следовательно, коэффициент диффузии тепловых нейтронов зависит не только от рассеивающих, но и от поглощающих свойств среды. Однако, как видно ниже, эта зависимость слаба, поскольку при сильном поглощении само уравнение (8.160) становится неприменимым (в силу неприменимости закона Фика), и коэффициент диффузии теряет физический смысл.

Приняв, что сечение поглощения 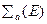изменяется с энергией нейтронов по закону 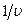,будем иметь

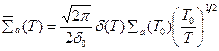; (8.164)

,

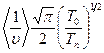где 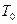— абсолютная температура, обычно соответствующая нормальной t = 20°C.

Уравнение (8.160), записанное относительно плотности нейтронов N=N(r, t), принимает следующий вид:

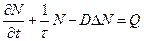, (8.165)

где

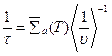. (8.166)

Величина 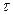, которая есть не что иное, как время жизни тепловых нейтронов, зависит от температуры среды только через плотность 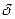(в случае 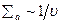)[6]

Коэффициент диффузии для плотности нейтронов

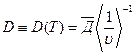. (8.167)

Подстановкой 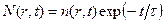уравнение (8.165) упрощается

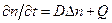(8.165)

и формально совпадает с уравнением возраста (28), по аналогии с решением которого функцию Грина G(r, t) нестационарного уравнения диффузии (79) с точечным мгновенным ( 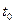= 0) изотропным источником тепловых нейтронов в безграничной изотропной среде можно написать сразу:

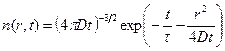. (8.166)

Пространственная дисперсия временного распределения равна (А.Эйнштейн, М.Смолуховский; 1905)

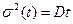, (8.167)

Общее для бесконечной однородной среды решение уравнения (8.165) .имеет следующий вид:

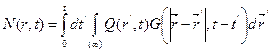. (8.168)

Используя свойство мультипликативности функции пространственно-временного распределения замедленных нейтронов, согласно которому Q (r, t) =Q(r)q(t), получим

.

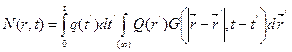Процесс замедления нейтронов протекает во времени гораздо быстрее процесса диффузии, детали кинетики замедления не могут влиять на временное распределение тепловых нейтронов. Приближенно можно считать, что источники тепловых нейтронов рождаются мгновенно, в момент, равный времени собственно замедления нейтронов до тепловой энергии:

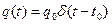, (8.169)

где 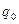— число нейтронов в импульсе генератора; 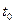— время собственно замедления до тепловой энергии, по малости которого можно положить 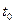= 0. Тогда

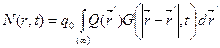. (8.170)

Величина интеграла (8.170) сравнительно слабо зависит от выбора функции Q(r) (особенно при больших t) . Беря Q(r) в возрастном приближении, имеем

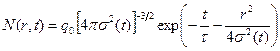, (8.171)

где 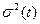— возраст тепловых нейтронов (дисперсия временного распределения N(r, t):

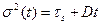, (8.167 )

причем 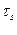— полный возраст до тепловой энергии. Выбор других обоснованных аппроксимаций Q(r) не меняет (при достаточно больших t) принципиальных свойств решения и влияет лишь на вид слагаемого, не зависящего от t, в выражении для 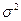. По этой причине фермиевский возраст в последнем выражении заменен полным.

Решение (8.171) обладает достаточно широкой областью применимости: при малом водородосодержании оно справедливо для произвольных r, t, при малых r — для произвольных времен (t> 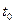) и водородосодержаний, при больших t — для произвольных водородосодержаний и расстояний от источника. Это отвечает физически ясному представлению о кинетике процессов замедления и диффузии нейтронов, в соответствии с которым при больших t пространственно-временное распределение тепловых нейтронов определяется процессом диффузии и практически нe зависит от первоначального их распределения. Поскольку в, системе скважина — пласт (при условии 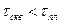) первоначальное распределение нейтронов определяется свойствами заполняющей скважину среды, фундаментальное простое решение (86) для бесконечной однородной изотропной среды имеет важное значение и представляет большой практический интерес.