ОДНОГРУППОВОЕ ДИФФУЗИОННОЕ ПРИБЛИЖЕНИЕ

В стационарных нейтронных методах применяют полиэнергетические радиоизотопные источники нейтронов, обладающие непрерывным спектром. В этом случае функция распределения 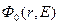определяется следующим образом:

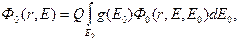(8.105)

где 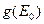- так называемая «весовая» функция спектра;

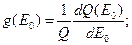
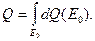(8.106)

Интегрирование ведется по всей области определения спектра.

На рис.8.5 приведены функции пространственного распределения нейтронов с фиксированной конечной энергией 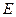,соответствующие отдельным спектральным полосам (линиям) спектра, и результирующее распределение, соответствующее всему спектру. Форма результирующего пространственного распределения отличается от формы распределений, порожденных отдельными спектральными линиями.

Это явление называется спектральным эффектом полиэнергетического источника и обусловлено тем, что вклад различных участков спектра в результирующую плотность потока нейтронов сильно изменяется с увеличением расстояния от источника. Если на малых расстояниях от источника основной вклад дает «мягкая» часть спектра, то на больших расстояниях определяющий вклад дает «жесткая» часть спектра. Иными словами, с точки зрения пространственного распределения нейтронов на больших расстояниях полиэнергетический источник как бы вырождается в жесткий моноэнергетический.

Рис. 8.5. Пространственное распределение нейтронов с заданной конечной энергией 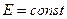от разных моноэнергетических источников (1) и результирующее распределение для полиэнергетического источника (2).

Благодаря спектральному эффекту, функция пространственного распределения нейтронов полиэнергетического источника приобретает более простую форму по сравнению с функциями распределения отдельных спектральных линий. В координатах 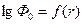она как бы «спрямляется» (линеаризуется).

Анализ результатов многочисленных экспериментов показал, что пространственное изменение плотности потока нейтронов полиэнергетических источников в различных средах (исключая малые водородосодержания) можно аппроксимировать простыми выражениями типа

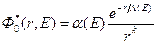, (8.107)

где k принимает значение 0 или 1.

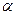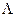Это распределение справедливо для практически важной: пространственной области — на средних и больших расстояниях: от источника. В выражении (24) имеются два свободных параметра и , для определения которых используются следующие точные условия:

1^о. 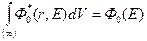(8.108)

(спектр плотности потока в бесконечной однородной среде с равномерно распределенными источниками; интегрирование распространено на весь бесконечный объем V). При отсутствии поглощения это просто закон сохранения числа замедленных нейтронов во всем бесконечном пространстве.

2^о. 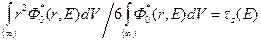, (8.108')

где 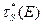— полный возраст нейтронов полиэнергетическог источника; 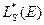— длина замедления нейтронов. Таким образом, интегральные характеристики приближенного распределения 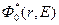должны совпадать с точными. Последние могут быть вычислены с учетом неупругого рассеяния и дифракционной анизотропии, а также спектра полиэнергетического источника. Условия (23) позволяют определить свободные параметры эмпирического распределения.

При k=0 определяя параметры 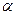и 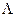, получаем (Я.Б.Зельдович, И.И.Гуревич):

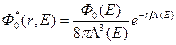, (8.109)

где

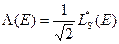. (8.109 )

Для изучения распределения нейтронов в горных породах эта формула впервые была применена С. А. Кантором (1955).

При k=1 распределение (24) называется «диффузионным» или «одногрупповым» ядром. Оно лучше согласуется с экспериментальными данными (особенно для водородсодержащих сред) и обладает более широкой областью применимости.

Определяя свободные параметры, как выше, находим

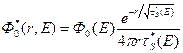. (8.110)

На рис.8.6 показаны результаты расчета пространственного распределения плотности потока надтепловых (индиевых) нейтронов Ra—Ве- источника в воде в одногрупповом диффузионном приближении в сравнении с экспериментальными данными. Практически на всех исследованных расстояниях r от источника (исключая окрестность источника) распределение (8.110) хорошо согласуется с экспериментальными данными.

Рис.8.6. Распределение индиевых нейтронов (Ra-Ве) - источника в воде в сравнении с результатами расчетов в одногрупповом диффузионном приближении (кривая 1) 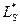=6,8 см. Кривая 2 иллюстрирует неправильное применение возрастного приближения (полный возраст нейтронов полиэнергетического источника отождествлен с фермиевским)

Это распределение имеет одно важное практическое преимущество, заключающееся в том, что оно удовлетворяет хорошо изученному дифференциальному уравнению второго порядка с постоянными коэффициентами:

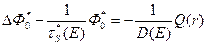. (8.111)

Уравнение (8.111) совпадает с уравнением диффузии, поэтому основанное на нем приближение (8.110) называют одногрупповым диффузионным приближением (ОДП). В этом приближении распределение замедленных нейтронов полиэнергетического источника (каждому участку энергетического спектра которого соответствует своя «группа» нейтронов) заменяется одной группой нейтронов, характеризующейся величиной .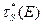

Численное решение этого уравнения с соответствующими краевыми и граничными условиями позволяет распространить рассмотренный способ приближенного описания пространственного распределения замедленных нейтронов в бесконечной однородной среде на более общий (и с практической точки зрения значительно более важный) случай системы скважина-пласт.

Величина 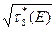(длина замедления нейтронов) играет роль диффузионной длины, а смысл коэффициента диффузии D(E) имеет величина

,

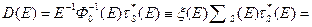
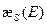
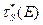где 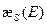— замедляющая способность среды.

Коснемся вопроса об условиях применимости решений уравнения (27). С одной стороны, уравнение диффузии предполагает выполнение закона Фика и неравенства

.

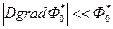Это означает, что уравнение (8.111) перестает быть справедливым, когда коэффициент диффузии и плотность потока нейтронов заметно изменяются на расстояниях порядка длины замедления. Последнее всегда имеет место вблизи границ раздела сред с различными нейтронными свойствами, что характерно для скважинных условий применения нейтронных методов. С другой стороны, аналогия уравнения (8.111) с уравнением диффузии является формальной, поэтому строгое ограничение уравнения диффузии не может механически переноситься на уравнение, которому удовлетворяет аппроксимирующее распределение.

Несмотря на свою простоту, ОДП позволяет сделать целый ряд практически полезных и важных выводов относительно закономерностей стационарных нейтронных методов в системе скважина-пласт.

Можно показать[3], что возраст 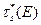и длина замедления 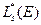нейтронов полиэнергетического источника равны возрасту и длине замедления нейтронов моноэнергетического источника с энергией 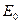, равной средней энергии 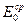спектра полиэнергетического источника:

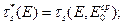(8.112)

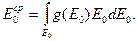(8.113)

Рис.8.7. Распределения по сфери­ческим слоям нейтронов индиевого резонанса 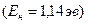Po-Be источника в воде (1) и кварцевом песке различной влажности (по экспериментальным данным А. В. Золотова): 35% (2), 7% (3), 3% (4).

Для более полного рас­крытия физиче­ско­го смысла параметра 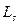рассмотрим функцию

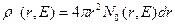, (8.114)

описывающую число нейтронов с заданной энергией 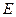в сферическом слое толщиной 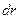на расстоянии 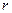от источника. При 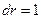эта функция характеризует пространственное распределение замедленных нейтронов в сферических слоях единичной толщины. Функция 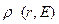обладает максимумом (рис.8.7) положение которого 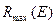легко найти из условия

,

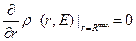из которого следует

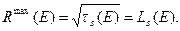(8.115)

Таким образом, длина замедления нейтронов равна расстоянию от источника до максимума функции распределения по сферическим слоям нейтронов с заданной энергией .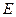

Значение 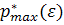функции p^*(r, ε) в максимуме будет:

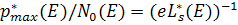
Отсюда следует, что при фиксированной конечной энергии Е с уменьшением замедляющей способности среды максимальная амплитуда функции 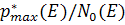убывает (амплитуда функции 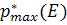возрастает).

Определим пространственную дисперсию D[(E)] функции p^*(r, E). По определению, D[(E)] равна:

D[(E)] = 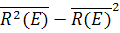. (8.116)

Здесь 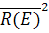- второй пространственный момент функции 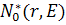, равный по определению:

,

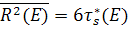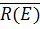- первый пространственный момент функции 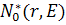, равный:

.

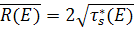Подставляя эти величины в (8.114), находим:

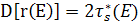. (8.117)

Итак, пространственная дисперсия функции распределения нейтронов по сферическим слоям равна удвоенному значению полного возраста нейтронов.

На рис.8.7 приведены распределения по сферическим слоям надтепловых нейтронов Po-Be источника в кварцевом песчанике с различной водонасы­щен­ной пористостью, построенные по экcпериментальным данным А.В.Золотовым (1956). Поскольку выражение (8.110) особенно хорошо описывает пространственное распределение нейтронов в средах с высоким водородсодержанием, для последних результат (8.115) обладает количественной достоверностью. Сравнивая расстояния до максимума этих распределений с соответствующими значениями длины замедления нейтронов P-Be источника в воде, можно убедиться, что это соотношение выполняется.

Для определения полного возраста (квадрата длины замедления) по результатам измерений обычно строят графики функций p(r;E) и r²p(r;E), и вычисляют площади, ограниченные полученными кривыми, после чего величина 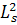определяется из отношений этих площадей:

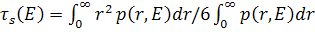. (8.118)