ДИФФУЗИЯ ТЕПЛОВЫХ НЕЙТРОНОВ

Процесс переноса нейтронов можно считать состоящим из этапов замедления, диффузии и переходного этапа — термализации.

На этапе термализации решающую роль играет неупругое молекулярное рассеяние, а также неупругое взаимодействие нейтронов с кристаллической решеткой, в результате которых нейтроны как теряют, так и приобретают энергию, причем обмен энергией определяется не только массой атомов и молекул, сечением взаимодействия, но также температурой среды и типом химической связи.

При слабом поглощении распределение тепловых нейтронов является результатом большого числа рассеяний. Обмен энергией между нейтронами и атомами замедлителя приводит систему нейтронный газ — атомы вещества в состояние термодинамического равновесия, при котором спектр нейтронов,f (Е. Т) описывается распределением Максвелла — Больцмана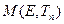

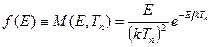(8.153)

с наиболее вероятной энергией

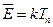, (8.154)

где 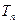— эффективная температура спектра тепловых нейтронов («температура нейтронов»); k — постоянная Больцмана.

Распределение (8.153) применимо для описания энергетического спектра атомов (молекул) вещества, которое находится в газообразном состоянии. В этом случае 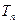совпадает с термодинамической температурой среды. Для замедлителей в твердом или жидком состоянии можно использовать две модели твердого тела, предложенные Эйнштейном и Дебаем для расчета удельной теплоемкости. В этих моделях распределение молекул по энергиям максвелловское, однако соответствующие температуры не совпадают с обычной термодинамической температурой Т. Различие температур является следствием квантово-механического эффекта, обусловленного дискретным спектром энергии; гармонических осцилляции молекул. Для типов связи, отличных от тех, которые подчиняются закону Гука, распределение молекул по энергии отличается от максвелловского, однако при высоких температурах величина 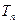совпадает с Т независимо от природы сил связи, а энергетический спектр подчиняется закону Максвелла.

Разновесный спектр нейтронов достигается в средах со слабым поглощением, в которых время жизни тепловых нейтронов больше времени термализации. Если время жизни тепловых нейтронов меньше времени термализации, замедленные нейтроны поглощаются, не достигнув равновесного состояния, и температура нейтронов превышает температуру замедлителя. При слабом поглощении спектр тепловых нейтронов практически не зависит от расстояния до источника с фермиевским спектром, и в любой точке однородной среды может быть описан спектром 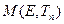в бесконечной среде с равномерно распределенными источниками.

Иными словами, для плотности потока тепловых нейтронов должно выполняться мультипликативное представление:

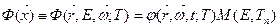. (8.155)

Рассмотрим уравнение переноса для тепловых нейтронов:

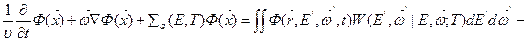
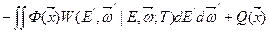. (8.156)

В этом уравнении интегрирование по энергии ведется от нуля до Е,где Е — «граничная», энергия, отделяющая область замедления от области термализации; 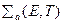— макроскопическое сечение поглощения:

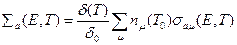
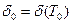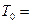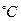(суммирование проводится по всем элементам смеси); ; 293 ; W( 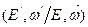; Т — индикатриса рассеяния тепловых нейтронов

,

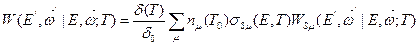нормированная условием

,

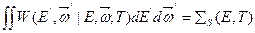где 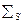— макроскопическое сечение рассеяния;

;

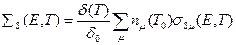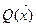— распределение источников тепловых нейтронов.

Энергетический спектр 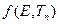удовлетворяет пространственно-однородному уравнению

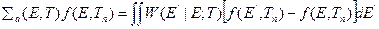. (8.157)

В поглощающих средах отклонение спектра тепловых нейтронов от максвелловского, определяется в основном не парамeтpaми индивидуального взaимoдeйcтвия, а соотношением поглощающих и рассеивающих свойств среды. В связи с этим для изучения спектра тепловых нейтронов в горных породах целесообразно пользоваться простейшей моделью замедлителя — моделью тяжелого одноатомного газа, основанной на предположении, что атомы вещества свободны и имеют лишь поступательную степень свободы (тепловое движение).

Введем функцию 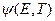, характеризующую отклонение энергетического спектра тепловых нейтронов 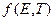в поглощающей среде от максвелловского спектра : .

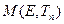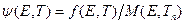Разложив 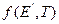в подынтегральном выражении (72)в ряд Тейлора, использовав принцип детального равновесия и выражения для энергетических моментов индикатрисы рассеяния, получаемой в модели тяжелого одноатомного газа, вместо (70)будем иметь следующее уравнение относительно , :

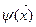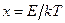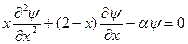, (8.158)

где 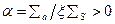( 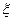— среднее изменение летаргии; 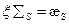— замедляющая способность вещества). Это уравнение определяет вырожденную гипергеометрическую функцию .

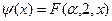Использовав асимптотическое представление 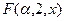по x, получим

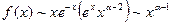
или

.

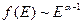Это значит, что резкой границы между энергетическими спектрами нейтронов в областях термализации и замедления (фермиевский спектр 1/Е при отсутствии поглощения, когда 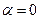), не существует. Если сечения захвата и рассеяния постоянны или одинаково зависят от энергии, то параметр α может быть определен по результатам измерений спектра надтепловых нейтронов, а также эффективной температуры спектра тепловых нейтронов (см. ниже).

Используя разложение 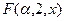при слабом поглощении, получим

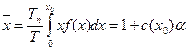, (8.159)

где 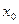— условная верхняя граница теплового спектра (в единицах kT). Следовательно,

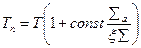. (8.159 )

Таким образом, температура линейно зависит от величины параметра .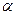

Поскольку время замедления нейтронов 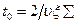и время их жизни относительно поглощения 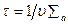, то

.

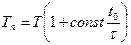Выражение (8.159)получено в приближении тяжелого одноатомного газа. Однако численные расчеты, а также экспериментыс водными растворами борной кислоты подтвердили, что эта зависимость сохраняется и при учете молекулярных эффектов. Особенности теоретической модели и физическое состояние замедлителя влияют только на величину константы c и на диапазон изменения параметра 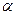, для которого справедливо установленное соотношение.

Рис.8.22. Зависимости температуры тепловых ней­тронов от параметра 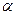в сухой (1) и заполненной водой (2) скважине d_c=110 мм (по Ш. А. Губерману и К. И. Якубсону).

Измерения температуры нейтронов на моделях пластов и в скважинах на месторождении боратов показали, что спектр тепловых нейтронов не зависит от размера зонда (расстояния до источника быстрых нейтронов) как в однородной среде, так и в скважинных условиях [17]. При измерениях в сухих скважинах 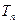характеризует замедляющие и поглощающие свойства породы по параметру 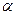(рис.8.22). К сожалению, заполнение скважины водой существенно снижает дифференциацию.