Минимизация функций в базисах И-НЕ и ИЛИ-НЕ
Функции " стрелка Пирса" (ИЛИ-НЕ) и "штрих Шеффера" (И-НЕ) обладают функциональной полнотой; для двух переменных:
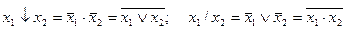
Для n переменных:
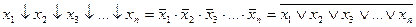
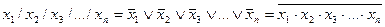
Эти соотношения позволяют свести задачу минимизации булевой функции в рассматриваемых базисах к задаче минимизации ДНФ и КНФ.
Для того, чтобы перейти от КНФ функции 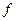 к выражению, представляющему функцию
к выражению, представляющему функцию 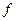 с помощью операции "стрелка Пирса" достаточно заменить в КНФ все операции конъюнкции и дизъюнкции операцией
с помощью операции "стрелка Пирса" достаточно заменить в КНФ все операции конъюнкции и дизъюнкции операцией 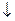 , сохранив скобки и отрицания на своих местах.
, сохранив скобки и отрицания на своих местах.
КНФ функции 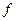 можно представить в общем виде:
можно представить в общем виде:
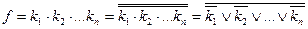
где 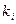 – элементарные дизъюнкции :
– элементарные дизъюнкции : 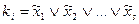 ;
; 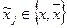
Используя операцию 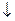 для n переменных, получим:
для n переменных, получим:
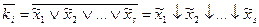
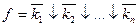
Таким образом, минимизацию функции можно осуществлять в базисе 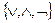 , а затем перейти к операции
, а затем перейти к операции 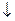 . Операция
. Операция 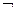 с помощью
с помощью 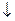 реализуется таким образом:
реализуется таким образом:
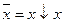
При переходе от многоместных операций к двухместным, необходимо учитывать, что функции 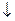 и / не подчиняются закону ассоциативности (
и / не подчиняются закону ассоциативности ( 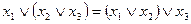 ;
; 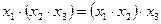 ). Если элементы только двухвходовые, то можно использовать следующие переходные соотношения:
). Если элементы только двухвходовые, то можно использовать следующие переходные соотношения:
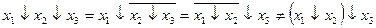
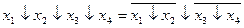
 |
Пример: рассмотрим функцию, заданную диаграммой Вейча:
 |
МКНФ: 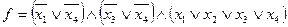
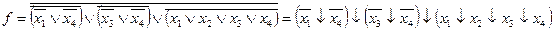
Переходя к двухместным операциям, получаем:
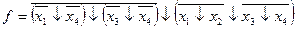
Аналогично осуществляется переход от произвольной ДНФ к выражению, содержащему только операцию "штрих Шеффера". Справедливы также переходные соотношения:
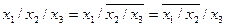
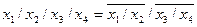
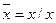
Пример:
МДНФ: 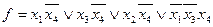
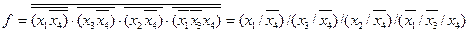
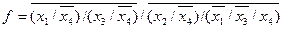
Дата добавления: 2016-07-18; просмотров: 3260;











