Минимизация систем булевых функций

Задача минимизации систем булевых функций хорошо исследована в ФПСБФ 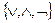Рассмотрим один из наиболее распространенных методов минимизации.

Пусть задана система полностью определенных булевых функций в ДНФ, например:

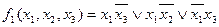
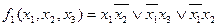
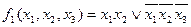
Все различные элементарные конъюнкции систем булевых функций объединим в множество А, которое назовем полным множеством элементарных конъюнкций системы булевых функций.

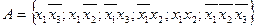
Система ДНФ булевых функций называется минимальной, если ее полное множество элементарных конъюнкций содержит минимальное количество букв, а каждая ДНФ булевых функций системы включает минимальное число элементарных конъюнкций наименьшего ранга. минимизация систем полностью определенных булевых функций может производиться по алгоритму, аналогичному алгоритму метода Квайна с небольшими отличиями.

Пример: пусть система булевых функций задана таблицей истинности. Найти МДНФ системы булевых функций.

Представим функции в СДНФ:

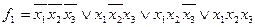
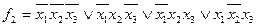
1. Построим полное множество А элементарных конъюнкций системы, указывая, какой функции принадлежит каждая конституэнта "1".

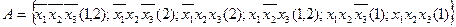
2. Построим СДНФ функции 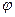, конституэнтами "1" которой являются все элементы множества А. Найдем СкДНФ функции .

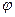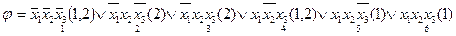
Выполним все склеивания:

1-2: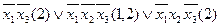

2-3: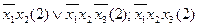

4-6: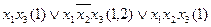

5-6: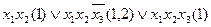

Если конституэнты единицы не принадлежат одной и той же функции системы, склеивание не производится.

Выполним все поглощения с учетом признака принадлежности каждой конъюнкции к функциям системы:

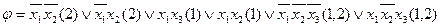
3. Строим импликантную матрицу Квайна.

- ядро функции :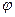

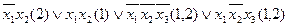
в данном случае ядро совпадает с МДНФ функции .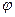

МДНФ системы булевых функций:

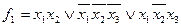
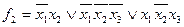
Недостаток метода: большая трудоемкость операций склеивания и поглощения с признаками.

Глава 9