Метод самопонижающихся циклов
 Метод самопонижающихся циклов позволяет получить СкДНФ булевой функции по специальным фрагментам ее таблицы истинности. Каждый фрагмент выделяется так, что может описываться только одной конъюнкцией. СкДНФ получается путем логического сложения конъюнкций, соответствующих фрагментам, при условии, что все выделенные фрагменты таблицы истинности булевой функции полностью покрывают ту ее часть, где булева функция =1.
Метод самопонижающихся циклов позволяет получить СкДНФ булевой функции по специальным фрагментам ее таблицы истинности. Каждый фрагмент выделяется так, что может описываться только одной конъюнкцией. СкДНФ получается путем логического сложения конъюнкций, соответствующих фрагментам, при условии, что все выделенные фрагменты таблицы истинности булевой функции полностью покрывают ту ее часть, где булева функция =1.
Если в таблице истинности произвольной булевой функции 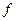 существует фрагмент вида (см. таблицу), то ее СкДНФ на этом фрагменте описывается выражением
существует фрагмент вида (см. таблицу), то ее СкДНФ на этом фрагменте описывается выражением 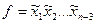 , так как по переменным
, так как по переменным 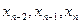 может быть произведено полное склеивание. Никаких ограничений на число склеенных переменных и размещение их во фрагменте таблицы истинности булевой функции не накладывается. Если имеется фрагмент, содержащий
может быть произведено полное склеивание. Никаких ограничений на число склеенных переменных и размещение их во фрагменте таблицы истинности булевой функции не накладывается. Если имеется фрагмент, содержащий 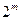 двоичных наборов длины n, где m – число склеенных переменных, то такой фрагмент описывается конъюнкцией ранга (n-m) в представлении булевой функции
двоичных наборов длины n, где m – число склеенных переменных, то такой фрагмент описывается конъюнкцией ранга (n-m) в представлении булевой функции 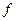 СкДНФ по этому фрагменту. Фрагмент вида (см. таблицу) называется самопонижающимся циклом, а число склеенных переменных во фрагменте – рангом самопонижающегося цикла.
СкДНФ по этому фрагменту. Фрагмент вида (см. таблицу) называется самопонижающимся циклом, а число склеенных переменных во фрагменте – рангом самопонижающегося цикла.
Пример:
Найти СкДНФ булевой функции 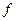 методом самопонижающихся циклов. Функция
методом самопонижающихся циклов. Функция 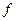 задана таблицей истинности.
задана таблицей истинности.

1. 
Ищем циклы максимального ранга 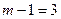 . Имеется только один такой цикл №1
. Имеется только один такой цикл №1 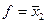 . Найденный цикл покрывает не все "1" таблицы истинности функции
. Найденный цикл покрывает не все "1" таблицы истинности функции 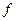 .
.
2. Ищем циклы ранга 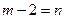 . Имеется два таких цикла №2 и №3. Цикл №3 полностью содержится в цикле №1, поэтому цикл №3 не рассматривается. Поиск цикла меньшего ранга не нужен, так как циклы 1 и 2 полностью покрывают конституэнты "1" функции
. Имеется два таких цикла №2 и №3. Цикл №3 полностью содержится в цикле №1, поэтому цикл №3 не рассматривается. Поиск цикла меньшего ранга не нужен, так как циклы 1 и 2 полностью покрывают конституэнты "1" функции 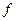 .
.
СкДНФ: 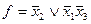
Дата добавления: 2016-07-18; просмотров: 2324;











