Метод Квайна-Мак-Класки

Метод формализован на этапе нахождения простых импликант. Формализация проводится таким образом:

1) Все конституэнты "1" из СДНФ булевой функции 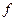записываются их двоичными номерами.

2) Все номера разбиваются на непересекающиеся группы, в i-ой группе находятся конституэнты "1", содержащие i единиц в номере.

3) Склеиваются только номера соседних групп, склеивание номера как-либо отмечают.

4) Производят все возможные склеивания. Неотмеченные после склеивания номера являются простыми импликантами.

Пример:

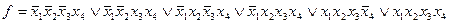
1) В СДНФ заменим все конституэнты "1" их двоичными номерами:

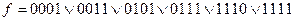
2) Образуем группы двоичных номеров и произведем склеивание:

Простые импликанты: *111, 111*, 0**1

МДНФ: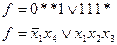

Разбиение конституэнт на группы позволяет уменьшить число парных сравнений при склеивании.

Метод Нельсона

Метод позволяет получить СкДНФ булевой функции 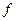из ее произвольной КНФ. Если в произвольной КНФ булевой функции 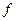раскрыть все скобки и произвести все поглощения, то в результате будет получена СкДНФ булевой функции .

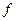Пример: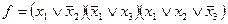

Найдем СкДНФ: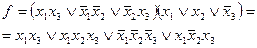

Произведем поглощения: 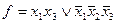- СкДНФ.