Абстрактная теория автоматов

Абстрактным автоматом называется дискретное устройство, задаваемое тремя непустыми множествами 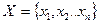, , 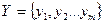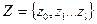называемыми алфавитами входных сигналов, выходных сигналов и состояний, и двумя функциями - функцией переходов 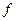, определяющей состояние автомата 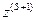в S+1-м такте в зависимости от состояния автомата 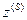и значения входной буквы 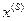в S-м такте

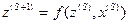
и функцией выходов 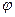, определяющей значение выходной буквы 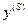в зависимости от состояния автомата 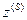и входной буквы 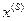в S -м такте

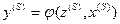
Обычно на множестве 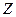фиксируется одно из состояний 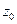в качестве начального (инициальный автомат).

По способу формирования функции выхода выделяют 3 типа абстрактных автоматов: автомат Мили, автомат Мура, С-автомат.

Эти автоматы описываются системой уравнений:

автомат Мили: автомат Мура:

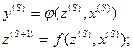
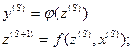
С-автомат:

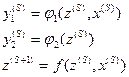
Будем рассматривать только автоматы детерминированного типа, у которых каждой паре 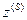и 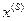однозначно соответствует пара 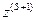и 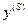. Функционирование детерминированных автоматов подчиняется следующим условиям:

- любому входному слову из 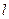букв (слову длиной 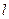) соответствует выходное слово той же длины,

- двум входным словам, в которых первые 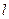букв совпадают, соответствуют выходные слова с совпадающими 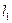первыми буквами, если перед подачей входных слов, автомат находился в одном и том же состоянии.

Функци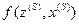и и 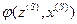, описывающие работу автомата Мили, можно задать с помощью таблиц переходов и выходов. По этим таблицам можно определить реакцию автомата на любое входное слово.

В таблице 1 приведены произвольная последовательность входных сигналов и соответствующие ей последовательности состояний и выходных сигналов автомата, заданного таблицей переходов и выходов.

Более наглядным является представление автоматов Мили с помощью графов. Граф автомата состоит из узлов (вершин) соединенных ветвями (ребрами). Узлы графа отождествляются с состояниями автомата, а ветви отмечаются входными сигналами, вызывающими переход автомата по данной ветви, и выходными сигналами, соответствующими такому переходу.

Два автомата, у которых совпадают как входные, так и выходные сигналы, называются эквивалентными. если для любого входного слова выходное слово одного автомата совпадает с выходным словом другого автомата.

Для любого автомата Мили можно построить эквивалентный автомат Мура и наоборот. Для этого:

1) поставим каждой паре 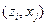автомата Мили состояние 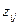автомата Мура;

2) во множество состояний автомата Мура включим начальное состояние 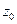автомата Мили. Если автомат Мили имеет 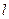состояний и 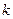входных сигналов, то эквивалентный автомат Мура будет иметь 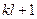состояний.

Из таблицы видно, что состояние 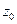автомата Мили совпадает с состояниями 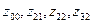автомата Мура, т.е.

, ,

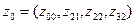
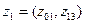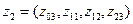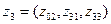
Значения функции выходов для эквивалентного автомата Мура определяются соотношением:

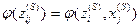при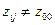

Для начального состояния 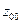значение выходного сигнала выбирается произвольно. Т.о. переходы и выходные сигналы эквивалентного автомата Мура определяются таблицей:

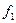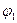Задача перехода от автомата Мура к эквивалентному автомату Мили решается очень просто. Если и – функции переходов и выходов автомата Мура, то функции переходов 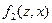и выходов 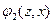эквивалентного автомата Мили определяются соотношениями:

;

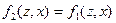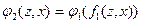
Т.о. таблица переходов эквивалентного автомата Мили совпадает с таблицей переходов автомата Мура, а таблица выходов составляется так, что в каждую ее клетку записывается сигнал, которым отмечено состояние в данной клетке.

Частичными автоматами называются автоматы, на входы которых некоторые последовательности сигналов никогда не подаются (запрещенные входные слова)

Основными задачами теории автоматов являются задачи анализа и синтеза автоматов. Под анализом автомата понимают установление закона его функционирования по заданной схеме автомата, под синтезом – построение автомата из более простых автоматов по заданному закону функционирования. При решении этих задач наиболее важными являются абстрактный и структурный этап.

На абстрактном этапе автомат задается таблицами или графом или каким-нибудь другим способом. На структурном этапе автомат понимают как структурную схему, состоящую из набора простейших автоматов и ФПС логических элементов.