Декомпозиция абстрактных автоматов

Под декомпозицией понимается представление абстрактного автомата совокупностью нескольких более простых автоматов.

Задача декомпозиции абстрактного автомата – это задача разложения автомата по алгебраическим операциям. В качестве операций обычно рассматриваются такие: умножение, суммирование, суперпозиция и композиция.

Рассмотри задание алгебраических операций умножения, суммирования, суперпозиции автоматов.

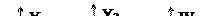Операция умножения двух автоматов А₁ и А₂ содержательно соответствует параллельной одновременной работе автоматов А₁ и А₂, т.е. подача на вход автомата А₃ входного сигнала 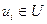соответствует тому, что на входы автоматов А₁ и А₂ одновременно и независимо друг от друга подаются входные сигналы 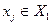и .

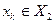Различают две модификации операции умножения. Первая, 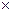, применяется к абстрактным автоматам А₁ и А₂ с различными входными алфавитами. Вторая, 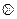, применяется к абстрактным автоматам А₁ и А₂, имеющим общий входной алфавит, и является частным случаем операции умножения.

Пример: Пусть автоматы А₁ и А₂ заданы графами.

Так как операция 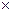соответствует одновременной параллельной работе двух А₁ и А₂ с раздельными входами, то построение графа А₃ можно описать таким образом: каждое 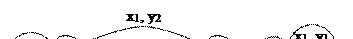состояние автомата А₃ будет однозначно соответствовать упорядоченной паре состояний автоматов А₁ и А₂. В начальный момент времени А₃ будет иметь состояние . Осуществляя перебор всех возможных комбинаций пар входных сигналов автоматов А₁ и А₂, получаем все возможные переходы автомата А₃.

Операция суммирования + двух автоматов А₁ и А₂ соответствует параллельной неодновременной работе автоматов А₁ и А₂; т.е. если задан автомат А₃=А₁+А₂, то любое входное слово автомата А₃ образуется чередованием входных букв А₁ и А₂, а любое выходное слово – чередованием выходных букв А₁ и А₂.

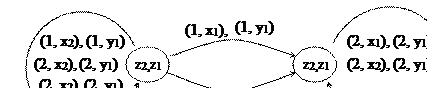Для автоматов А₁ и А₂, приведенных выше, операция + будет представлена следующим образом:

Операция суперпозиции соответствует последовательной работе автоматов А₁ и А₂

Построим автомат А₃=А₁*А₂

Глава 10

Структурная теория автоматов